7 Moving Beyond Linearity

7.1 Conceptual

7.1.1 Question 1

It was mentioned in the chapter that a cubic regression spline with one knot at \(\xi\) can be obtained using a basis of the form \(x, x^2, x^3, (x-\xi)^3_+\), where \((x-\xi)^3_+ = (x-\xi)^3\) if \(x>\xi\) and equals 0 otherwise. We will now show that a function of the form \[ f(x)=\beta_0 +\beta_1x+\beta_2x^2 +\beta_3x^3 +\beta_4(x-\xi)^3_+ \] is indeed a cubic regression spline, regardless of the values of \(\beta_0, \beta_1, \beta_2, \beta_3,\beta_4\).

  1. Find a cubic polynomial \[ f_1(x) = a_1 + b_1x + c_1x^2 + d_1x^3 \] such that \(f(x) = f_1(x)\) for all \(x \le \xi\). Express \(a_1,b_1,c_1,d_1\) in terms of \(\beta_0, \beta_1, \beta_2, \beta_3, \beta_4\).

In this case, for \(x \le \xi\), the cubic polynomial simply has terms \(a_1 = \beta_0\), \(b_1 = \beta_1\), \(c_1 = \beta_2\), \(d_1 = \beta_3\)

  1. Find a cubic polynomial \[ f_2(x) = a_2 + b_2x + c_2x^2 + d_2x^3 \] such that \(f(x) = f_2(x)\) for all \(x > \xi\). Express \(a_2, b_2, c_2, d_2\) in terms of \(\beta_0, \beta_1, \beta_2, \beta_3, \beta_4\). We have now established that \(f(x)\) is a piecewise polynomial.

For \(x \gt \xi\), the cubic polynomial would be (we include the \(\beta_4\) term). \[\begin{align} f(x) = & \beta_0 + \beta_1x + \beta_2x^2 + \beta_3x^3 + \beta_4(x-\xi)^3 \\ = & \beta_0 + \beta_1x + \beta_2x^2 + + \beta_4(x^3 - 3x^2\xi + 3x\xi^2 -\xi^3) \\ = & \beta_0 - \beta_4\xi^3 + (\beta_1 + 3\beta_4\xi^2)x + (\beta_2 - 3\beta_4\xi)x^2 + (\beta_3 + \beta_4)x^3 \end{align}\]

Therefore, \(a_1 = \beta_0 - \beta_4\xi^3\), \(b_1 = \beta_1 + 3\beta_4\xi^2\), \(c_1 = \beta_2 - 3\beta_4\xi\), \(d_1 = \beta_3 + \beta_4\)

  1. Show that \(f_1(\xi) = f_2(\xi)\). That is, \(f(x)\) is continuous at \(\xi\).

To do this, we replace \(x\) with \(\xi\) in the above equations and simplify.

\[\begin{align} f_1(\xi) = \beta_0 + \beta_1\xi + \beta_2\xi^2 + \beta_3\xi^3 \end{align}\]

\[\begin{align} f_2(\xi) = & \beta_0 - \beta_4\xi^3 + (\beta_1 + 3\beta_4\xi^2)\xi + (\beta_2 - 3\beta_4\xi)\xi^2 + (\beta_3 + \beta_4)\xi^3 \\ = & \beta_0 - \beta_4\xi^3 + \beta_1\xi + 3\beta_4\xi^3 + \beta_2\xi^2 - 3\beta_4\xi^3 + \beta_3\xi^3 + \beta_4\xi^3 \\ = & \beta_0 + \beta_1\xi + \beta_2\xi^2 + \beta_3\xi^3 \end{align}\]

  1. Show that \(f_1'(\xi) = f_2'(\xi)\). That is, \(f'(x)\) is continuous at \(\xi\).

To do this we differentiate the above with respect to \(x\).

\[ f_1'(x) = \beta_1 + 2\beta_2x + 3\beta_3x^2 f_1'(\xi) = \beta_1 + 2\beta_2\xi + 3\beta_3\xi^2 \]

\[\begin{align} f_2'(x) & = \beta_1 + 3\beta_4\xi^2 + 2(\beta_2 - 3\beta_4\xi)x + 3(\beta_3 + \beta_4)x^2 \\ f_2'(\xi) & = \beta_1 + 3\beta_4\xi^2 + 2(\beta_2 - 3\beta_4\xi)\xi + 3(\beta_3 + \beta_4)\xi^2 \\ & = \beta_1 + 3\beta_4\xi^2 + 2\beta_2\xi - 6\beta_4\xi^2 + 3\beta_3\xi^2 + 3\beta_4\xi^2 \\ & = \beta_1 + 2\beta_2\xi + 3\beta_3\xi^2 \end{align}\]

  1. Show that \(f_1''(\xi) = f_2''(\xi)\). That is, \(f''(x)\) is continuous at \(\xi\).

Therefore, \(f(x)\) is indeed a cubic spline.

\[ f_1'(x) = 2\beta_2x + 6\beta_3x \\ f_1''(\xi) = 2\beta_2\xi + 6\beta_3\xi \]

\[ f_2''(x) = 2\beta_2 - 6\beta_4\xi + 6(\beta_3 + \beta_4)x \\ \] \[\begin{align} f_2''(\xi) & = 2\beta_2 - 6\beta_4\xi + 6\beta_3\xi + 6\beta_4\xi \\ & = 2\beta_2 + 6\beta_3\xi \end{align}\]

Hint: Parts (d) and (e) of this problem require knowledge of single-variable calculus. As a reminder, given a cubic polynomial \[f_1(x) = a_1 + b_1x + c_1x^2 + d_1x^3,\] the first derivative takes the form \[f_1'(x) = b_1 + 2c_1x + 3d_1x^2\] and the second derivative takes the form \[f_1''(x) = 2c_1 + 6d_1x.\]

7.1.2 Question 2

Suppose that a curve \(\hat{g}\) is computed to smoothly fit a set of \(n\) points using the following formula: \[ \DeclareMathOperator*{\argmin}{arg\,min} % Jan Hlavacek \hat{g} = \argmin_g \left(\sum_{i=1}^n (y_i - g(x_i))^2 + \lambda \int \left[ g^{(m)}(x) \right]^2 dx \right), \] where \(g^{(m)}\) represents the \(m\)th derivative of \(g\) (and \(g^{(0)} = g\)). Provide example sketches of \(\hat{g}\) in each of the following scenarios.

  1. \(\lambda=\infty, m=0\).

Here we penalize the \(g\) and a infinite \(\lambda\) means that this penalty dominates. This means that the \(\hat{g}\) will be 0.

  1. \(\lambda=\infty, m=1\).

Here we penalize the first derivative (the slope) of \(g\) and a infinite \(\lambda\) means that this penalty dominates. Thus the slope will be 0 (and otherwise best fitting \(x\), i.e. at the mean of \(x\)).

  1. \(\lambda=\infty, m=2\).

Here we penalize the second derivative (the change of slope) of \(g\) and a infinite \(\lambda\) means that this penalty dominates. Thus the line will be straight (and otherwise best fitting \(x\)).

  1. \(\lambda=\infty, m=3\).

Here we penalize the third derivative (the change of the change of slope) of \(g\) and a infinite \(\lambda\) means that this penalty dominates. In other words, the curve will have a consistent rate of change (e.g. a quadratic function or similar).

  1. \(\lambda=0, m=3\).

Here we penalize the third derivative, but a value of \(\lambda = 0\) means that there is no penalty. As a result, the curve is able to interpolate all points.

7.1.3 Question 3

Suppose we fit a curve with basis functions \(b_1(X) = X\), \(b_2(X) = (X - 1)^2I(X \geq 1)\). (Note that \(I(X \geq 1)\) equals 1 for \(X \geq 1\) and 0 otherwise.) We fit the linear regression model \[Y = \beta_0 +\beta_1b_1(X) + \beta_2b_2(X) + \epsilon,\] and obtain coefficient estimates \(\hat{\beta}_0 = 1, \hat{\beta}_1 = 1, \hat{\beta}_2 = -2\). Sketch the estimated curve between \(X = -2\) and \(X = 2\). Note the intercepts, slopes, and other relevant information.

x <- seq(-2, 2, length.out = 1000)
f <- function(x) 1 + x + -2 * (x - 1)^2 * I(x >= 1)
plot(x, f(x), type = "l")
grid()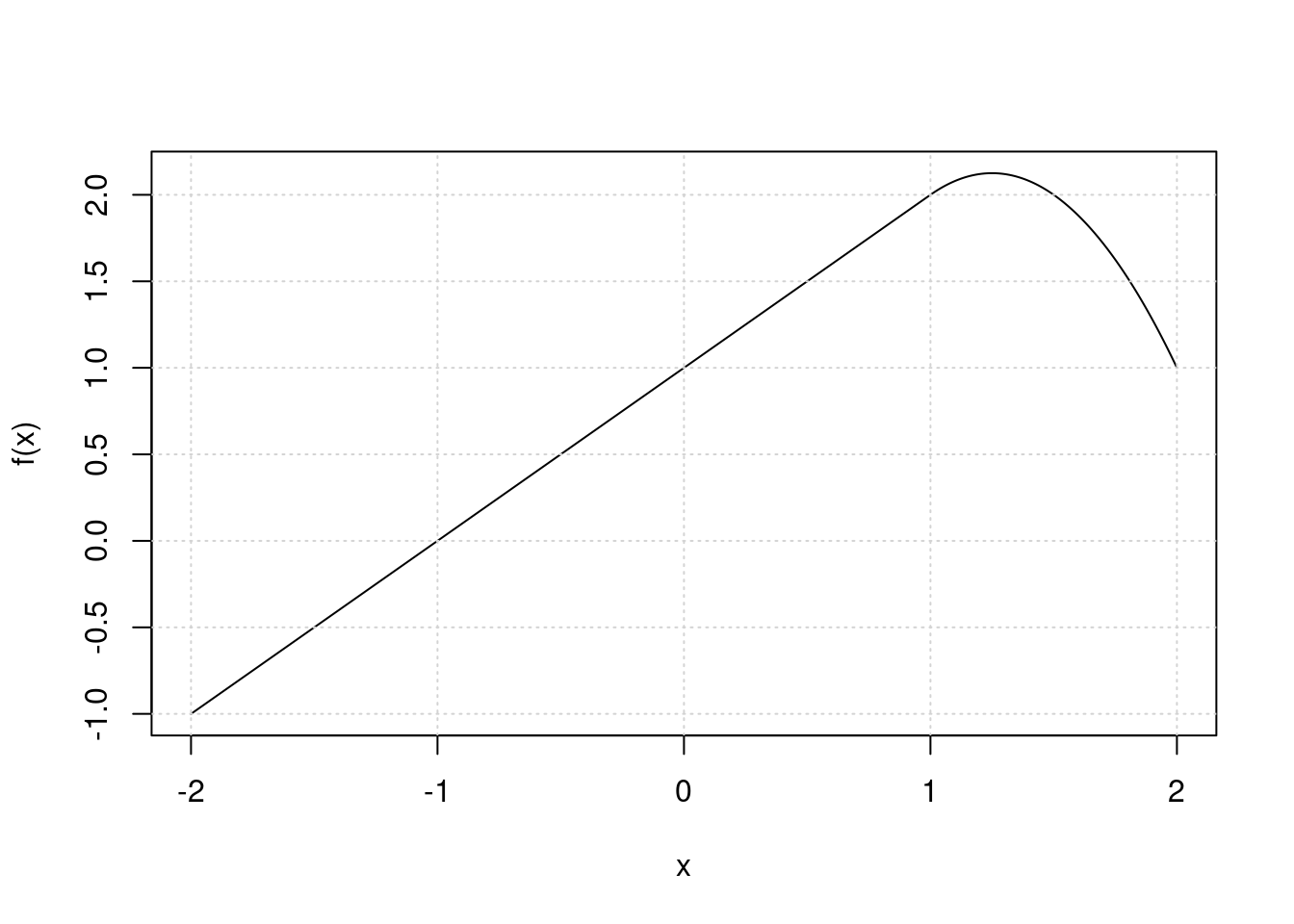

7.1.4 Question 4

Suppose we fit a curve with basis functions \(b_1(X) = I(0 \leq X \leq 2) - (X -1)I(1 \leq X \leq 2),\) \(b_2(X) = (X -3)I(3 \leq X \leq 4) + I(4 \lt X \leq 5)\). We fit the linear regression model \[Y = \beta_0 +\beta_1b_1(X) + \beta_2b_2(X) + \epsilon,\] and obtain coefficient estimates \(\hat{\beta}_0 = 1, \hat{\beta}_1 = 1, \hat{\beta}_2 = 3\). Sketch the estimated curve between \(X = -2\) and \(X = 6\). Note the intercepts, slopes, and other relevant information.

x <- seq(-2, 6, length.out = 1000)
b1 <- function(x) I(0 <= x & x <= 2) - (x - 1) * I(1 <= x &  x <= 2)
b2 <- function(x) (x - 3) * I(3 <= x  & x <= 4) + I(4 < x & x <= 5)
f <- function(x) 1 + 1*b1(x) + 3*b2(x)
plot(x, f(x), type = "l")
grid()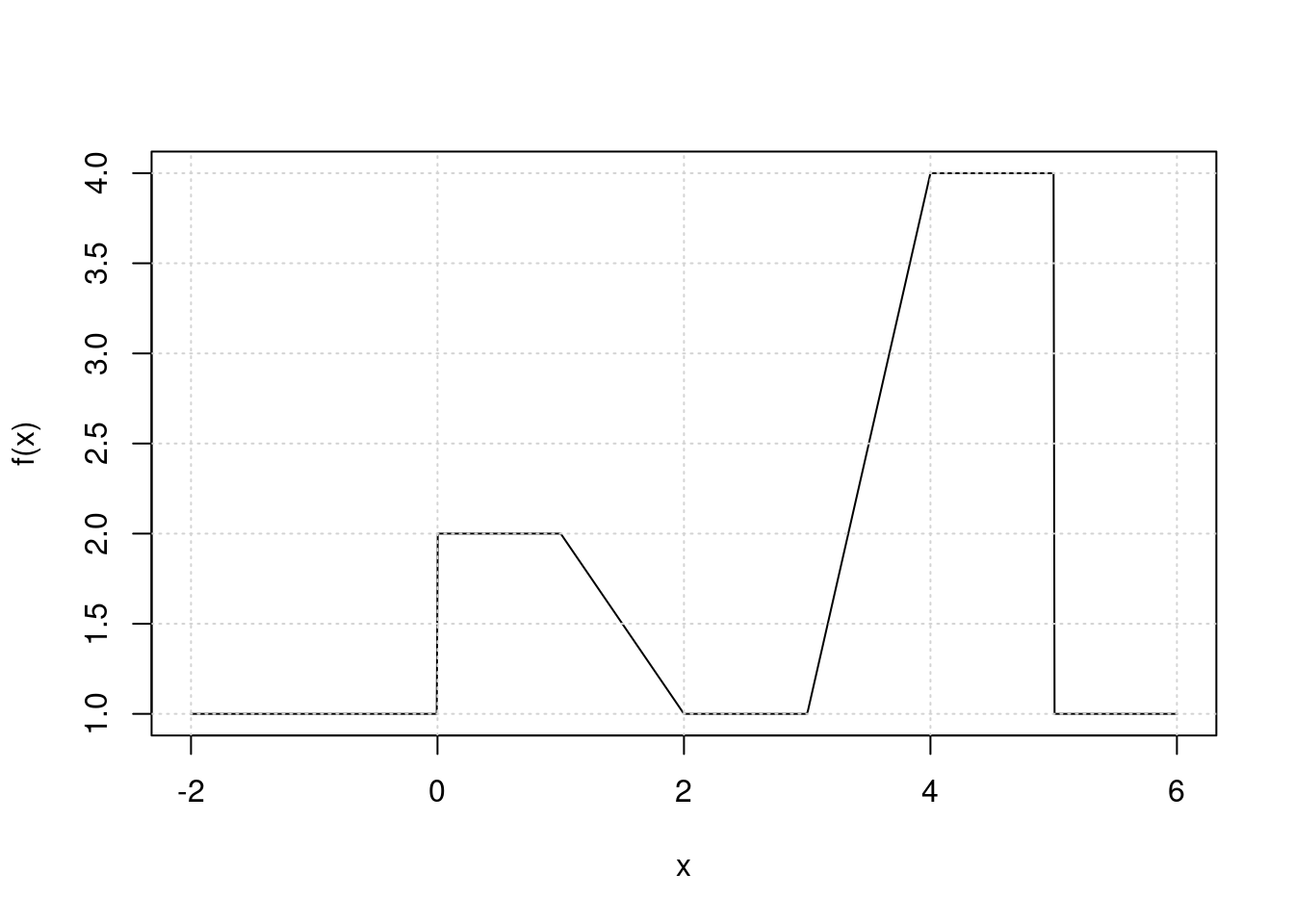

7.1.5 Question 5

Consider two curves, \(\hat{g}\) and \(\hat{g}_2\), defined by

\[ \hat{g}_1 = \argmin_g \left(\sum_{i=1}^n (y_i - g(x_i))^2 + \lambda \int \left[ g^{(3)}(x) \right]^2 dx \right), \] \[ \hat{g}_2 = \argmin_g \left(\sum_{i=1}^n (y_i - g(x_i))^2 + \lambda \int \left[ g^{(4)}(x) \right]^2 dx \right), \]

where \(g^{(m)}\) represents the \(m\)th derivative of \(g\).

  1. As \(\lambda \to \infty\), will \(\hat{g}_1\) or \(\hat{g}_2\) have the smaller training RSS?

\(\hat{g}_2\) is more flexible (by penalizing a higher derivative of \(g\)) and so will have a smaller training RSS.

  1. As \(\lambda \to \infty\), will \(\hat{g}_1\) or \(\hat{g}_2\) have the smaller test RSS?

We cannot tell which function will produce a smaller test RSS, but there is chance that \(\hat{g}_1\) will if \(\hat{g}_2\) overfits the data.

  1. For \(\lambda = 0\), will \(\hat{g}_1\) or \(\hat{g}_2\) have the smaller training and test RSS?

When \(\lambda = 0\) there is no penalty, so both functions will give the same result: perfect interpolation of the training data. Thus training RSS will be 0 but test RSS could be high.

7.2 Applied

7.2.1 Question 6

In this exercise, you will further analyze the Wage data set considered throughout this chapter.

  1. Perform polynomial regression to predict wage using age. Use cross-validation to select the optimal degree \(d\) for the polynomial. What degree was chosen, and how does this compare to the results of hypothesis testing using ANOVA? Make a plot of the resulting polynomial fit to the data.
library(ISLR2)
library(boot)
library(ggplot2)
set.seed(42)
res <- sapply(1:6, function(i) {
  fit <- glm(wage ~ poly(age, i), data = Wage)
  cv.glm(Wage, fit, K = 5)$delta[1]
})
which.min(res)
## [1] 6
plot(1:6, res, xlab = "Degree", ylab = "Test MSE", type = "l")
abline(v = which.min(res), col = "red", lty = 2)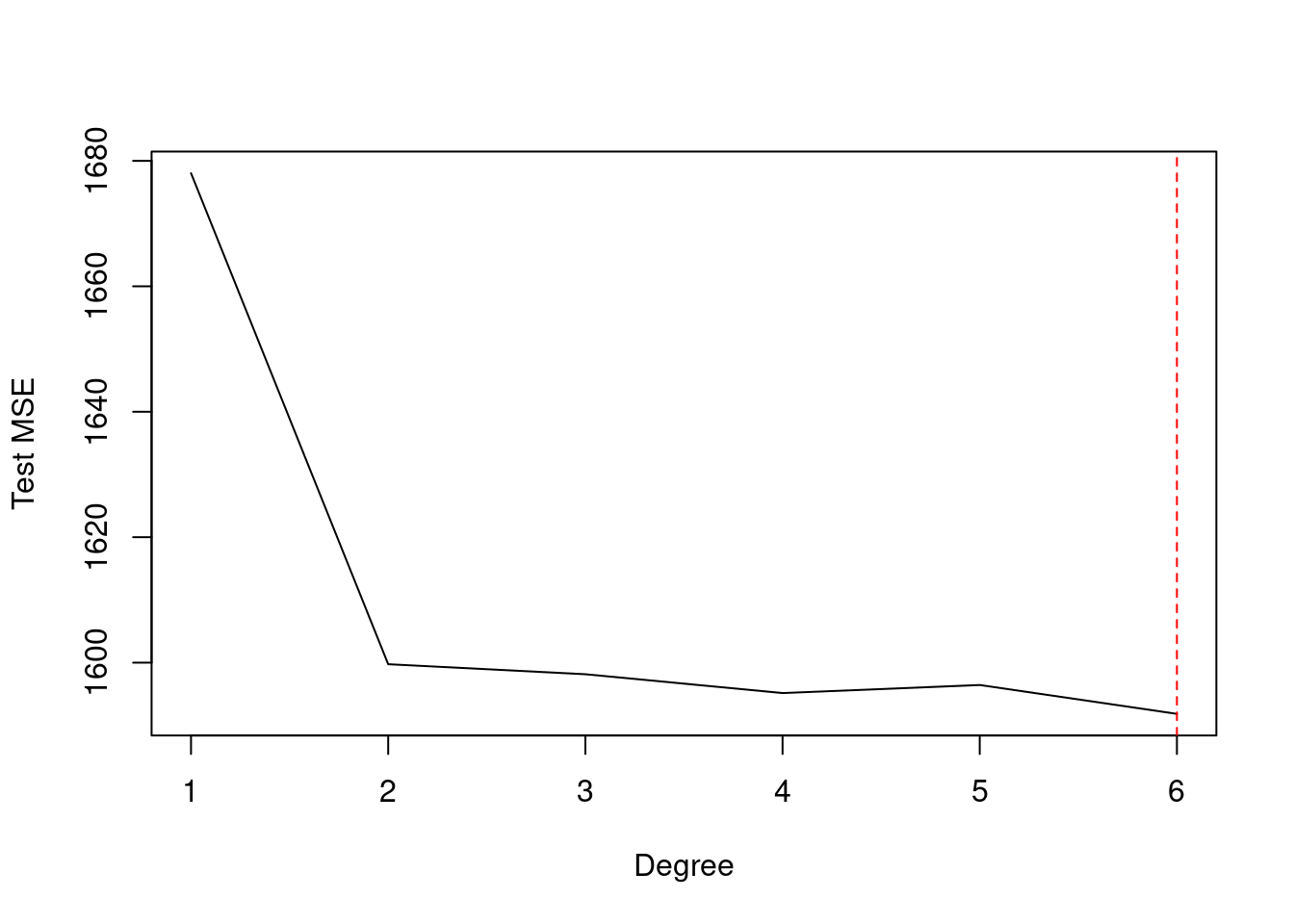

fit <- glm(wage ~ poly(age, which.min(res)), data = Wage)
plot(Wage$age, Wage$wage, pch = 19, cex = 0.4, col = alpha("steelblue", 0.4))
points(1:100, predict(fit, data.frame(age = 1:100)), type = "l", col = "red")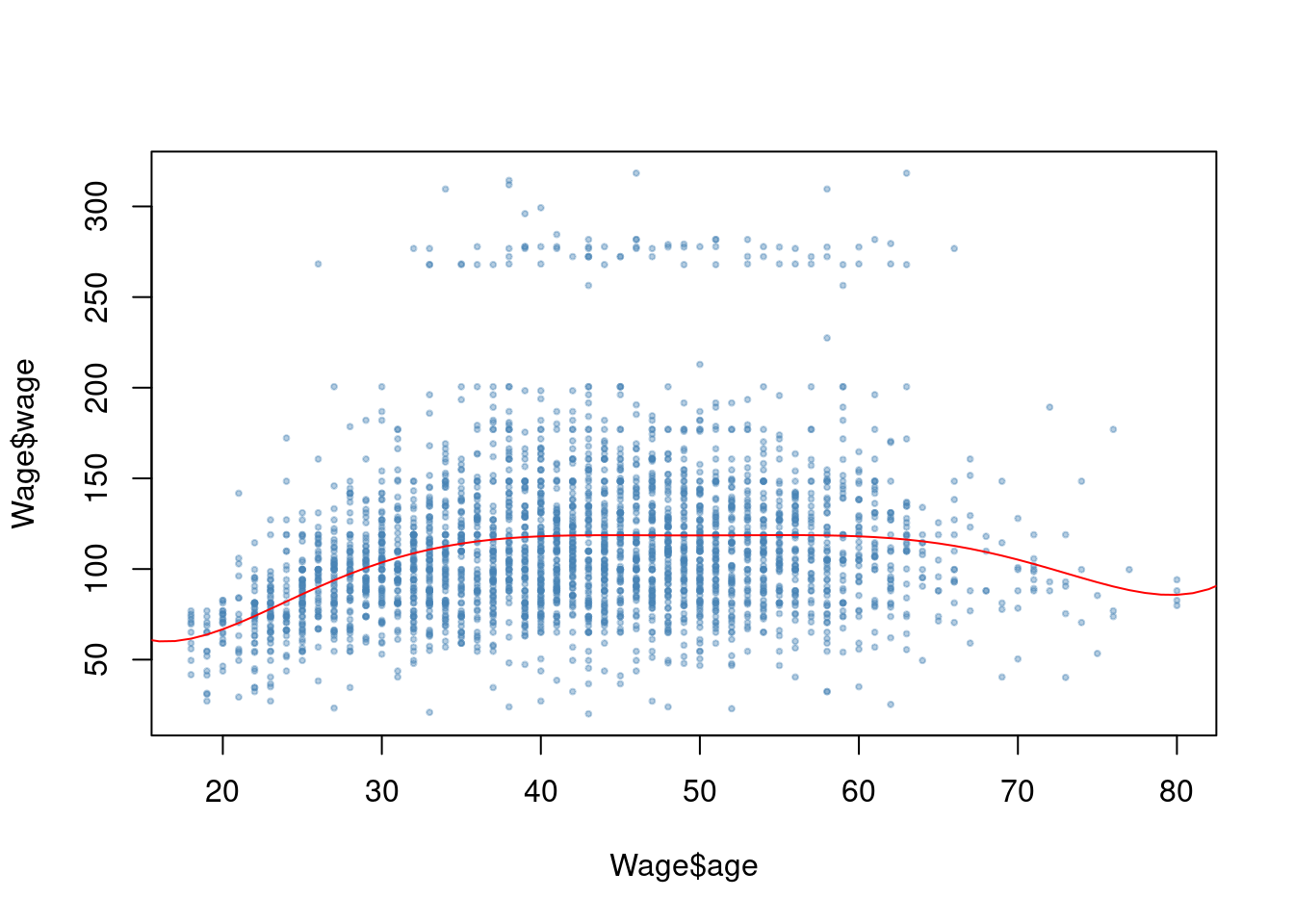

summary(glm(wage ~ poly(age, 6), data = Wage))
## 
## Call:
## glm(formula = wage ~ poly(age, 6), data = Wage)
## 
## Coefficients:
##                Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    111.7036     0.7286 153.316  < 2e-16 ***
## poly(age, 6)1  447.0679    39.9063  11.203  < 2e-16 ***
## poly(age, 6)2 -478.3158    39.9063 -11.986  < 2e-16 ***
## poly(age, 6)3  125.5217    39.9063   3.145  0.00167 ** 
## poly(age, 6)4  -77.9112    39.9063  -1.952  0.05099 .  
## poly(age, 6)5  -35.8129    39.9063  -0.897  0.36956    
## poly(age, 6)6   62.7077    39.9063   1.571  0.11620    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for gaussian family taken to be 1592.512)
## 
##     Null deviance: 5222086  on 2999  degrees of freedom
## Residual deviance: 4766389  on 2993  degrees of freedom
## AIC: 30642
## 
## Number of Fisher Scoring iterations: 2
fit1 <- lm(wage ~ poly(age, 1), data = Wage)
fit2 <- lm(wage ~ poly(age, 2), data = Wage)
fit3 <- lm(wage ~ poly(age, 3), data = Wage)
fit4 <- lm(wage ~ poly(age, 4), data = Wage)
fit5 <- lm(wage ~ poly(age, 5), data = Wage)
anova(fit1, fit2, fit3, fit4, fit5)
## Analysis of Variance Table
## 
## Model 1: wage ~ poly(age, 1)
## Model 2: wage ~ poly(age, 2)
## Model 3: wage ~ poly(age, 3)
## Model 4: wage ~ poly(age, 4)
## Model 5: wage ~ poly(age, 5)
##   Res.Df     RSS Df Sum of Sq        F    Pr(>F)    
## 1   2998 5022216                                    
## 2   2997 4793430  1    228786 143.5931 < 2.2e-16 ***
## 3   2996 4777674  1     15756   9.8888  0.001679 ** 
## 4   2995 4771604  1      6070   3.8098  0.051046 .  
## 5   2994 4770322  1      1283   0.8050  0.369682    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

The selected degree is 4. When testing with ANOVA, degrees 1, 2 and 3 are highly significant and 4 is marginal.

  1. Fit a step function to predict wage using age, and perform cross-validation to choose the optimal number of cuts. Make a plot of the fit obtained.
set.seed(42)
res <- sapply(2:10, function(i) {
  Wage$cats <- cut(Wage$age, i)
  fit <- glm(wage ~ cats, data = Wage)
  cv.glm(Wage, fit, K = 5)$delta[1]
})
names(res) <- 2:10
plot(2:10, res, xlab = "Cuts", ylab = "Test MSE", type = "l")
which.min(res)
## 8 
## 7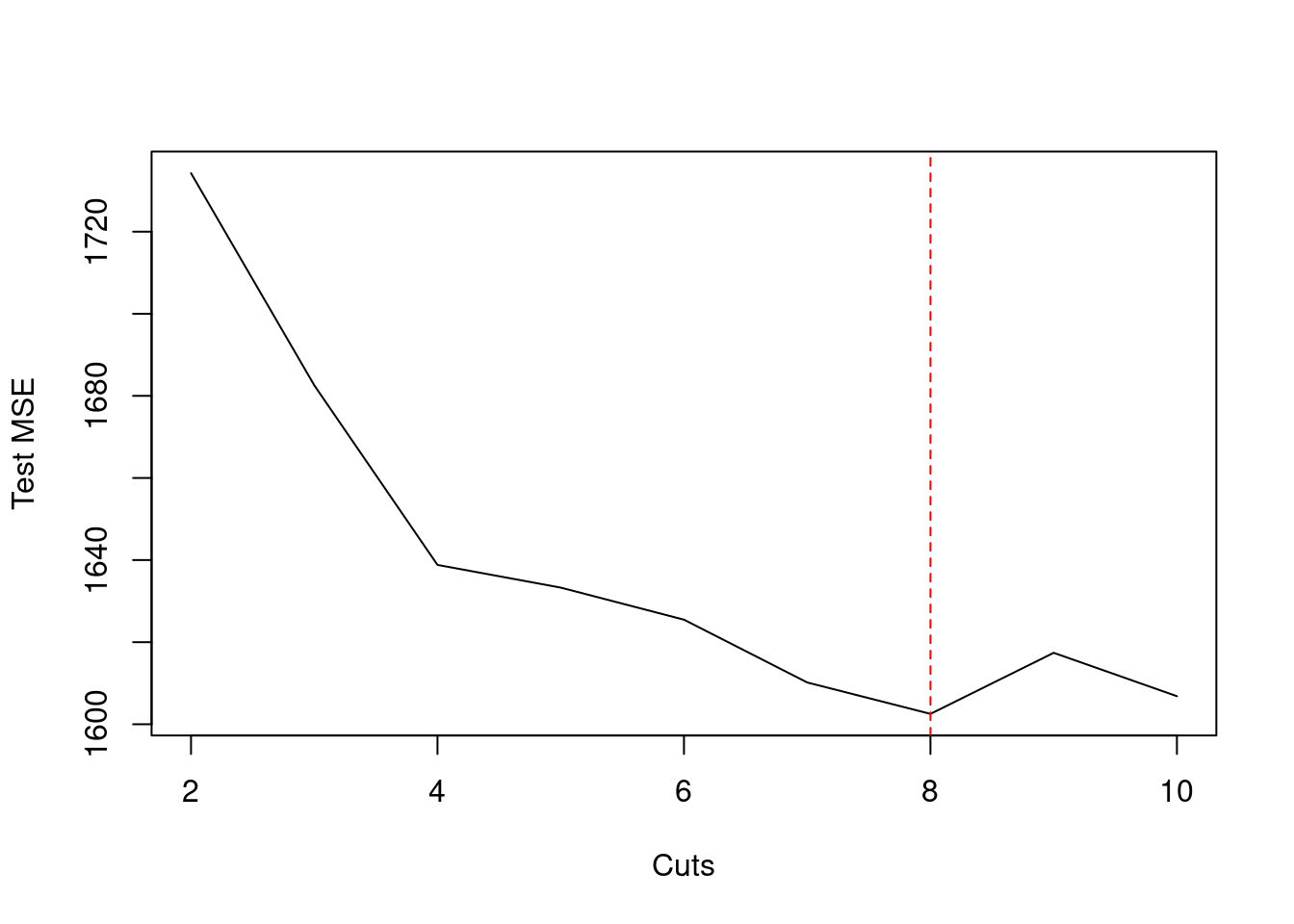
abline(v = names(which.min(res)), col = "red", lty = 2)

fit <- glm(wage ~ cut(age, 8), data = Wage)
plot(Wage$age, Wage$wage, pch = 19, cex = 0.4, col = alpha("steelblue", 0.4))
points(18:80, predict(fit, data.frame(age = 18:80)), type = "l", col = "red")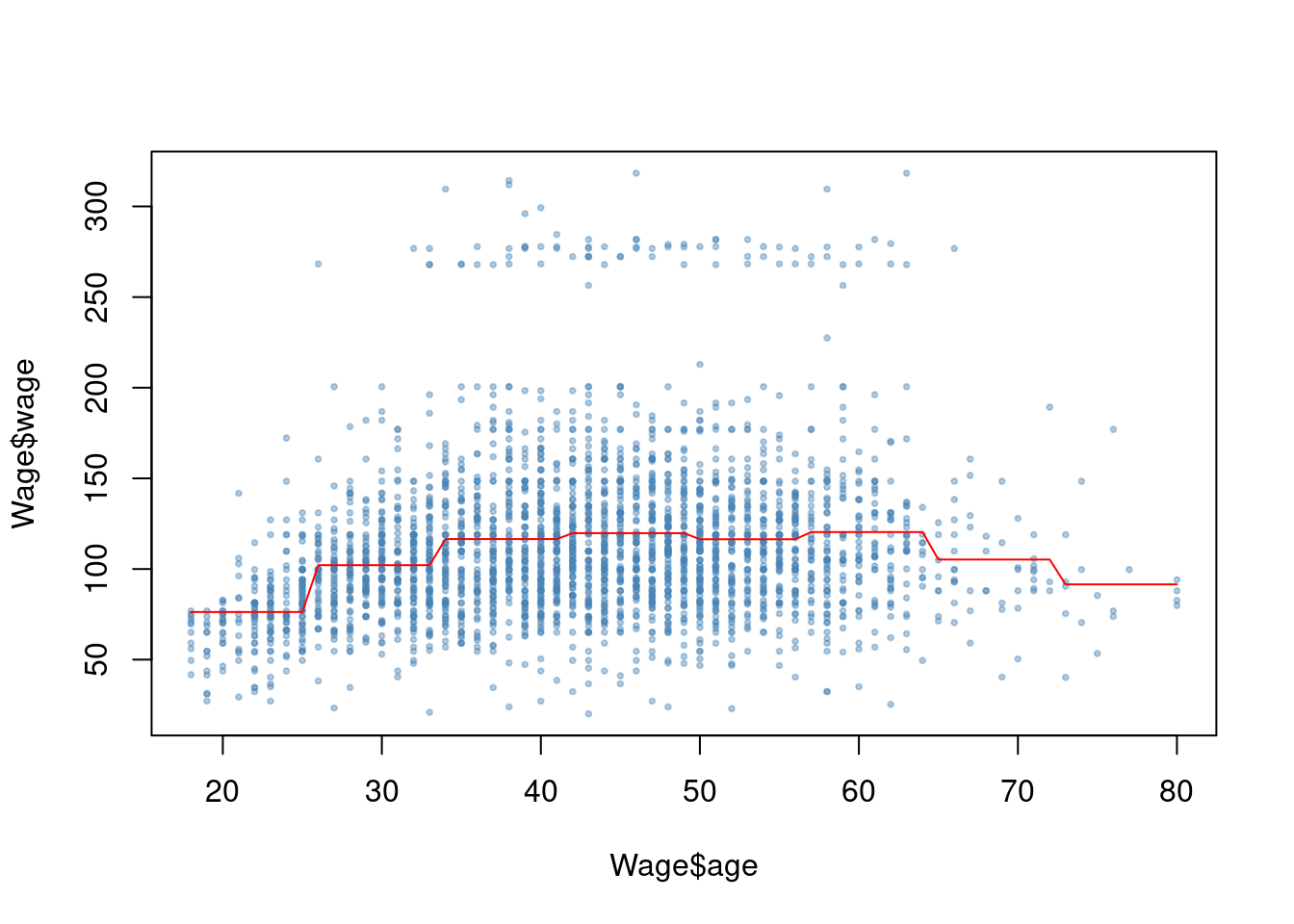

7.2.2 Question 7

The Wage data set contains a number of other features not explored in this chapter, such as marital status (maritl), job class (jobclass), and others. Explore the relationships between some of these other predictors and wage, and use non-linear fitting techniques in order to fit flexible models to the data. Create plots of the results obtained, and write a summary of your findings.

plot(Wage$year, Wage$wage, pch = 19, cex = 0.4, col = alpha("steelblue", 0.4))

plot(Wage$age, Wage$wage, pch = 19, cex = 0.4, col = alpha("steelblue", 0.4))

plot(Wage$maritl, Wage$wage, pch = 19, cex = 0.4, col = alpha("steelblue", 0.4))

plot(Wage$jobclass, Wage$wage, pch = 19, cex = 0.4, col = alpha("steelblue", 0.4))

plot(Wage$education, Wage$wage, pch = 19, cex = 0.4, col = alpha("steelblue", 0.4))

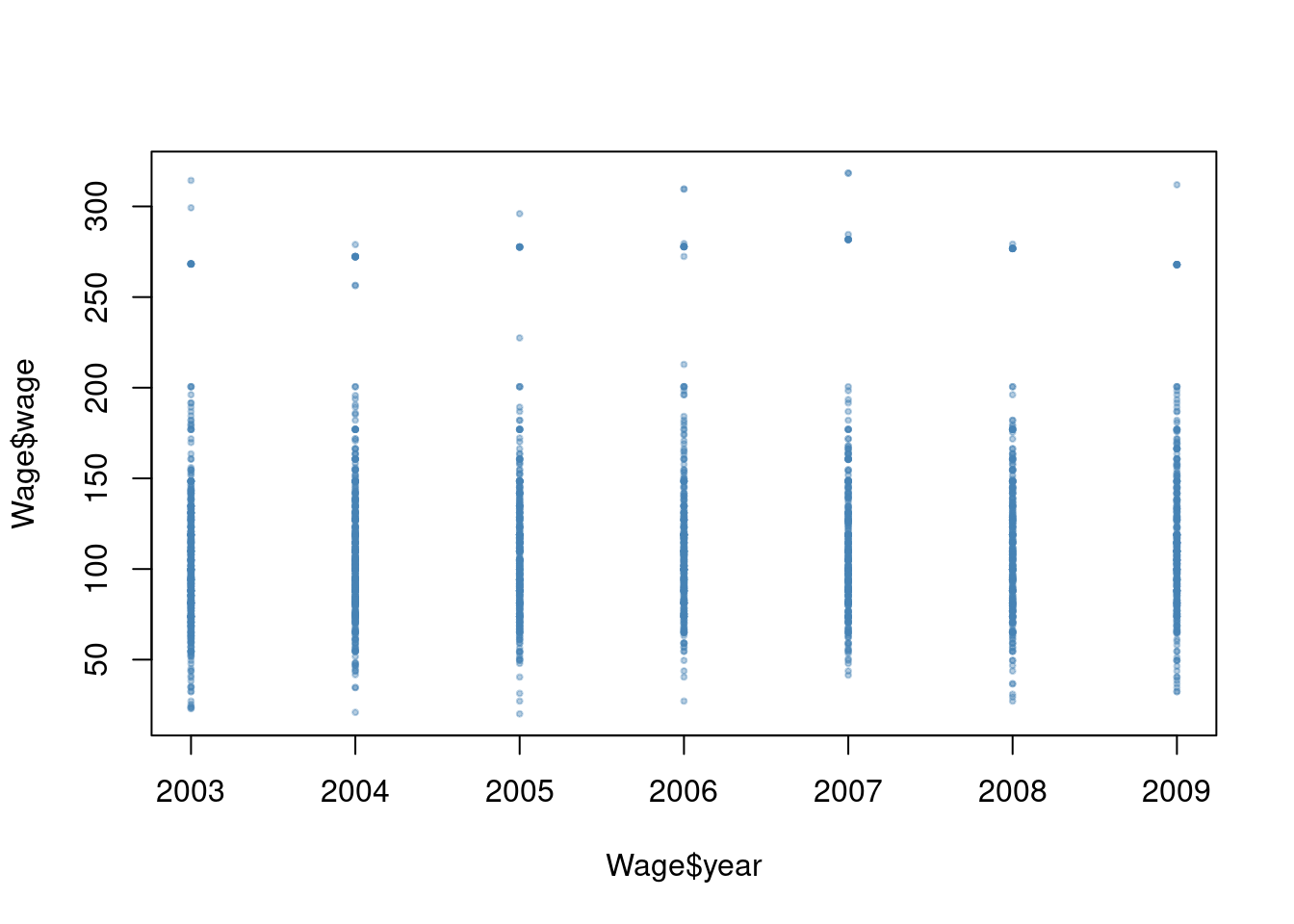
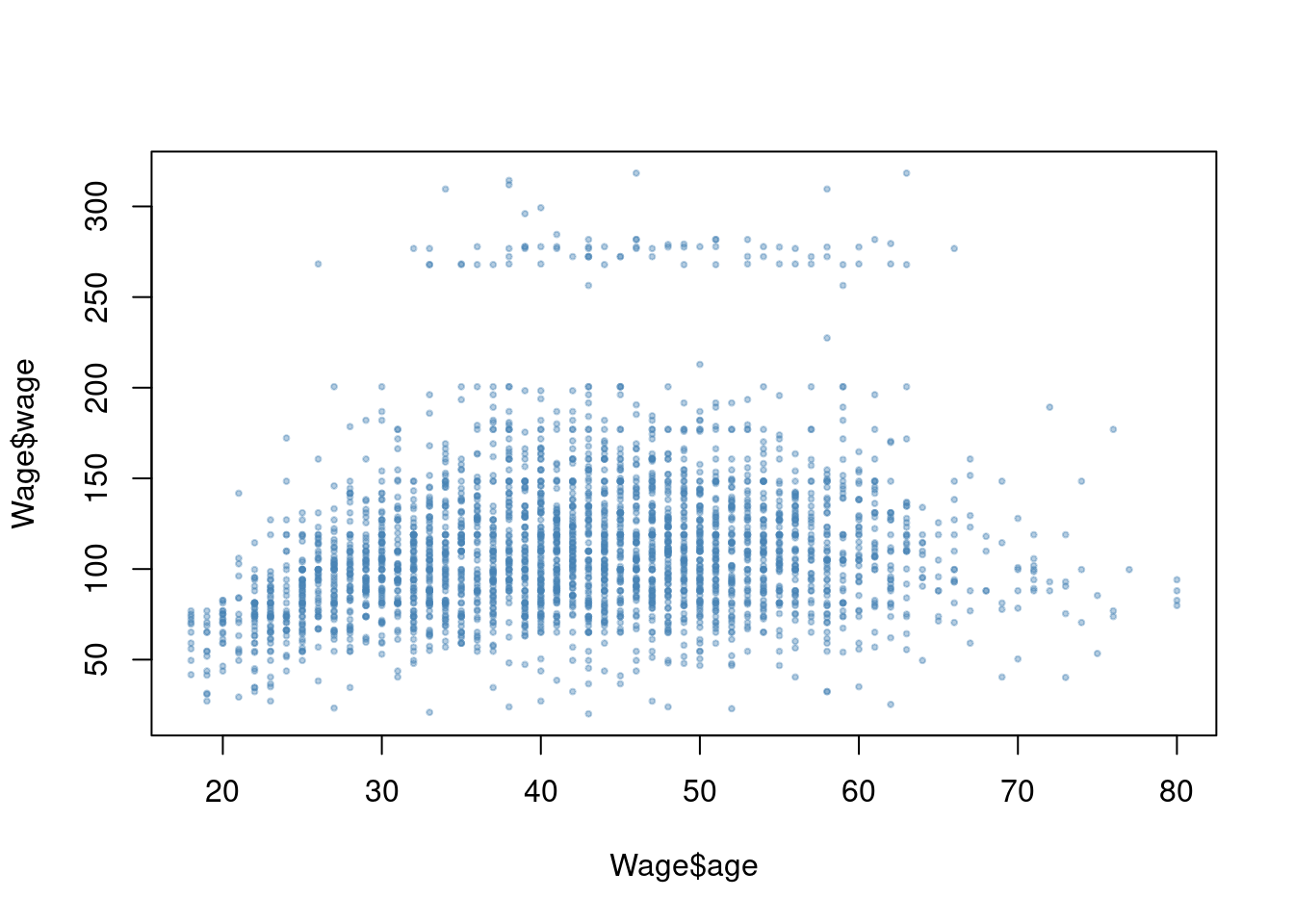
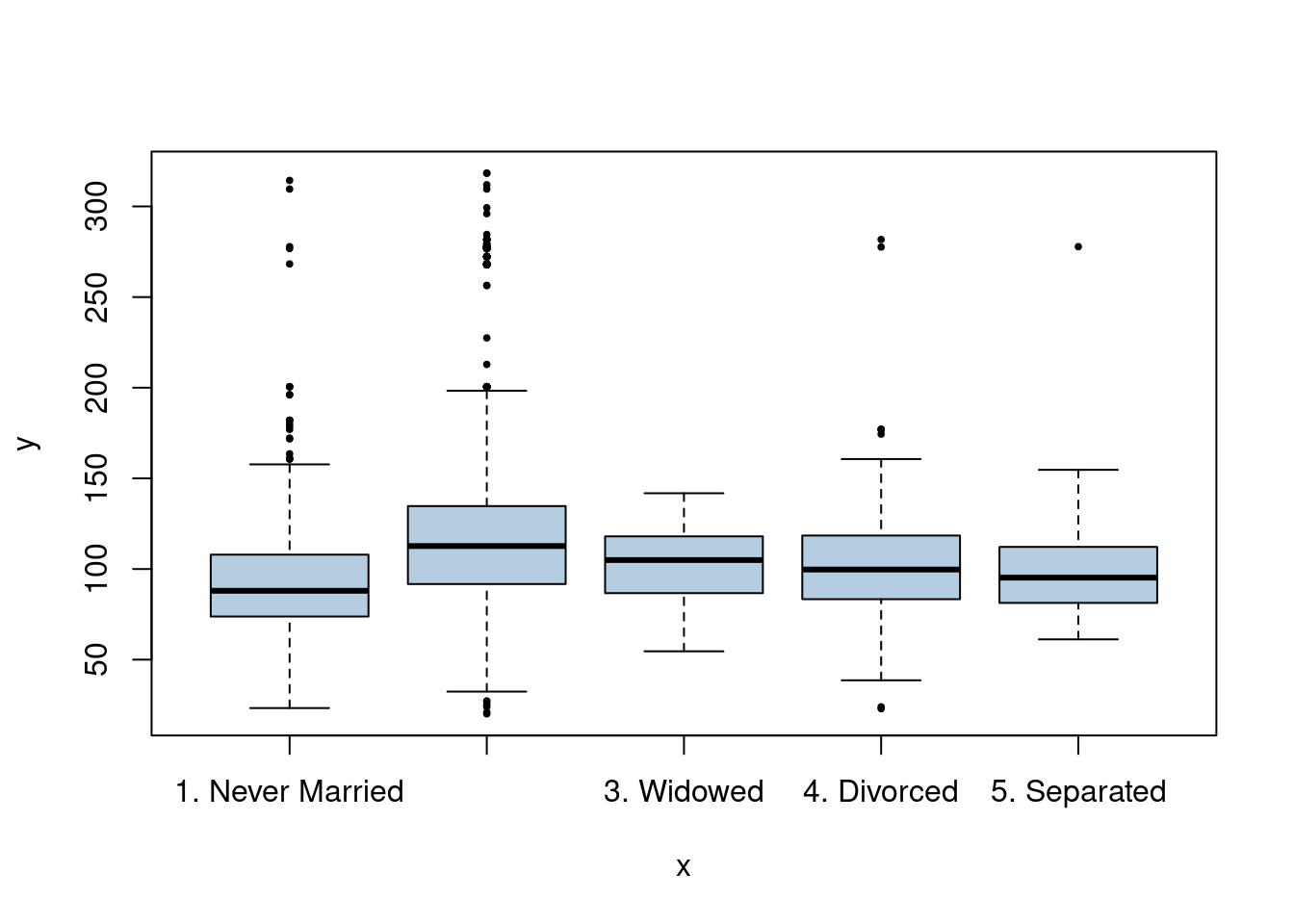
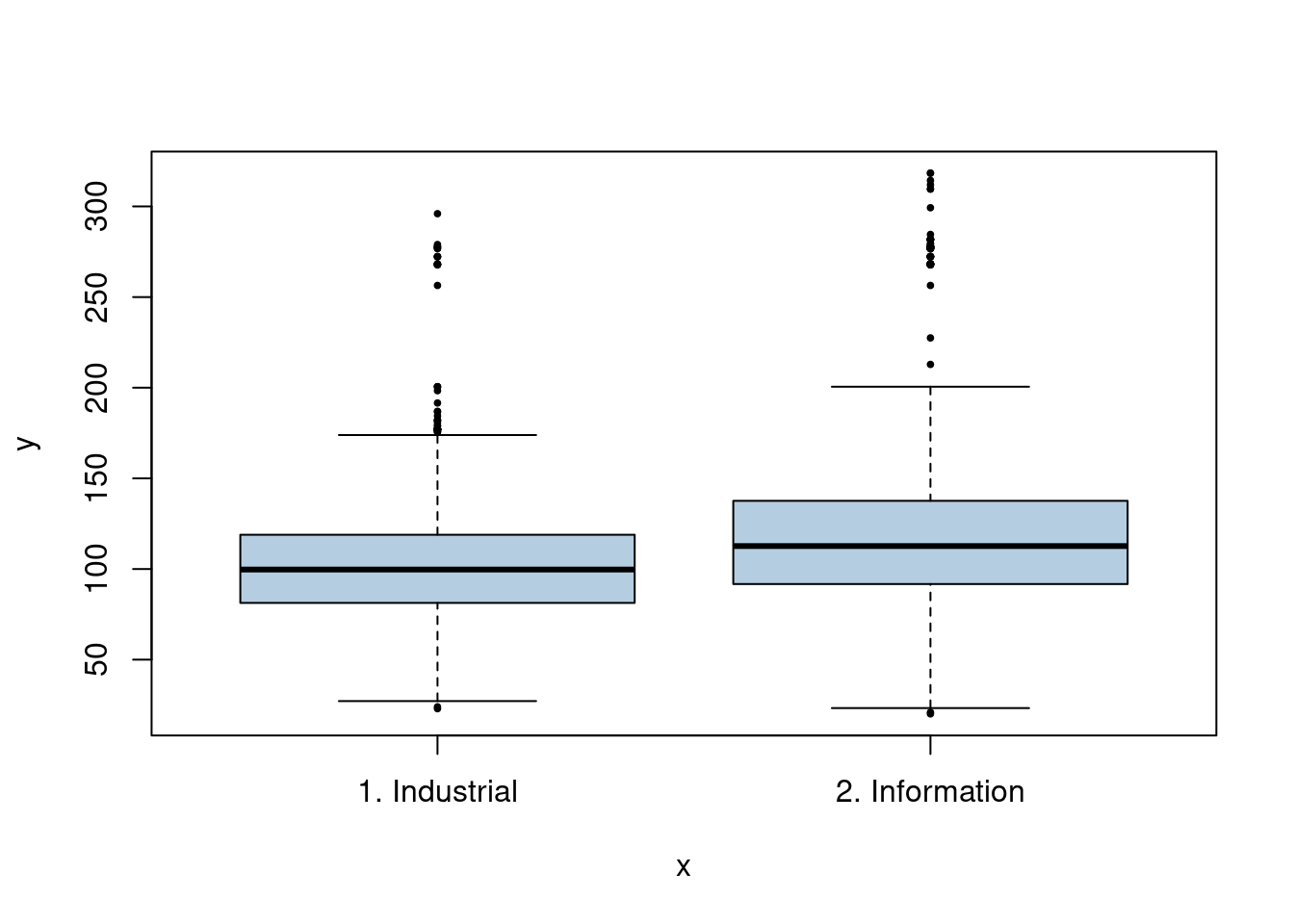
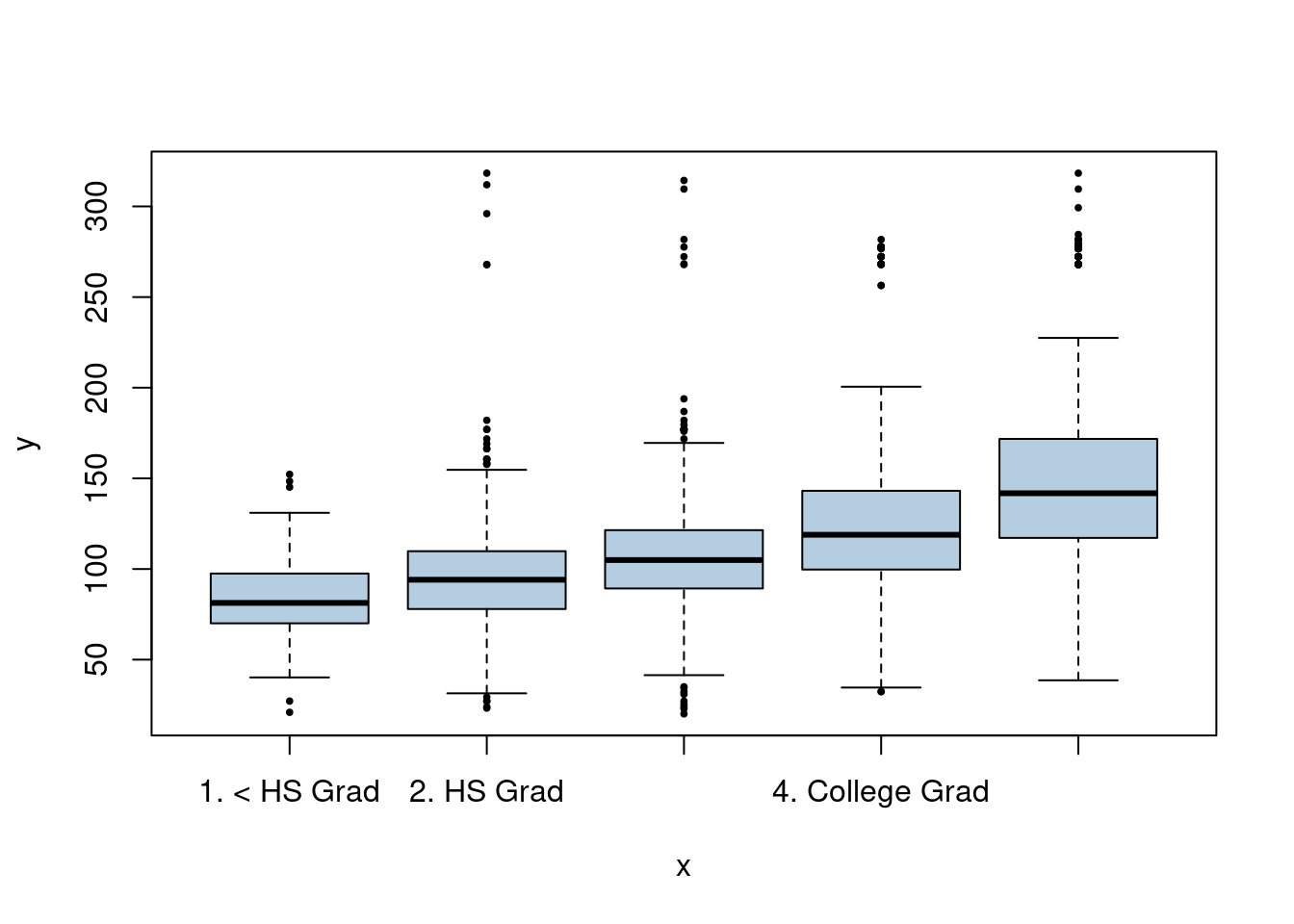
We have a mix of categorical and continuous variables and also want to incorporate non-linear aspects of the continuous variables. A GAM is a good choice to model this situation.

library(gam)
## Loading required package: splines
## Loading required package: foreach
## Loaded gam 1.22-4
fit0 <- gam(wage ~ s(year, 4) + s(age, 5) + education, data = Wage)
fit2 <- gam(wage ~ s(year, 4) + s(age, 5) + education + maritl, data = Wage)
fit1 <- gam(wage ~ s(year, 4) + s(age, 5) + education + jobclass, data = Wage)
fit3 <- gam(wage ~ s(year, 4) + s(age, 5) + education + jobclass + maritl, data = Wage)
anova(fit0, fit1, fit2, fit3)
## Analysis of Deviance Table
## 
## Model 1: wage ~ s(year, 4) + s(age, 5) + education
## Model 2: wage ~ s(year, 4) + s(age, 5) + education + jobclass
## Model 3: wage ~ s(year, 4) + s(age, 5) + education + maritl
## Model 4: wage ~ s(year, 4) + s(age, 5) + education + jobclass + maritl
##   Resid. Df Resid. Dev Df Deviance  Pr(>Chi)    
## 1      2986    3689770                          
## 2      2985    3677553  1    12218 0.0014286 ** 
## 3      2982    3595688  3    81865 1.071e-14 ***
## 4      2981    3581781  1    13907 0.0006687 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1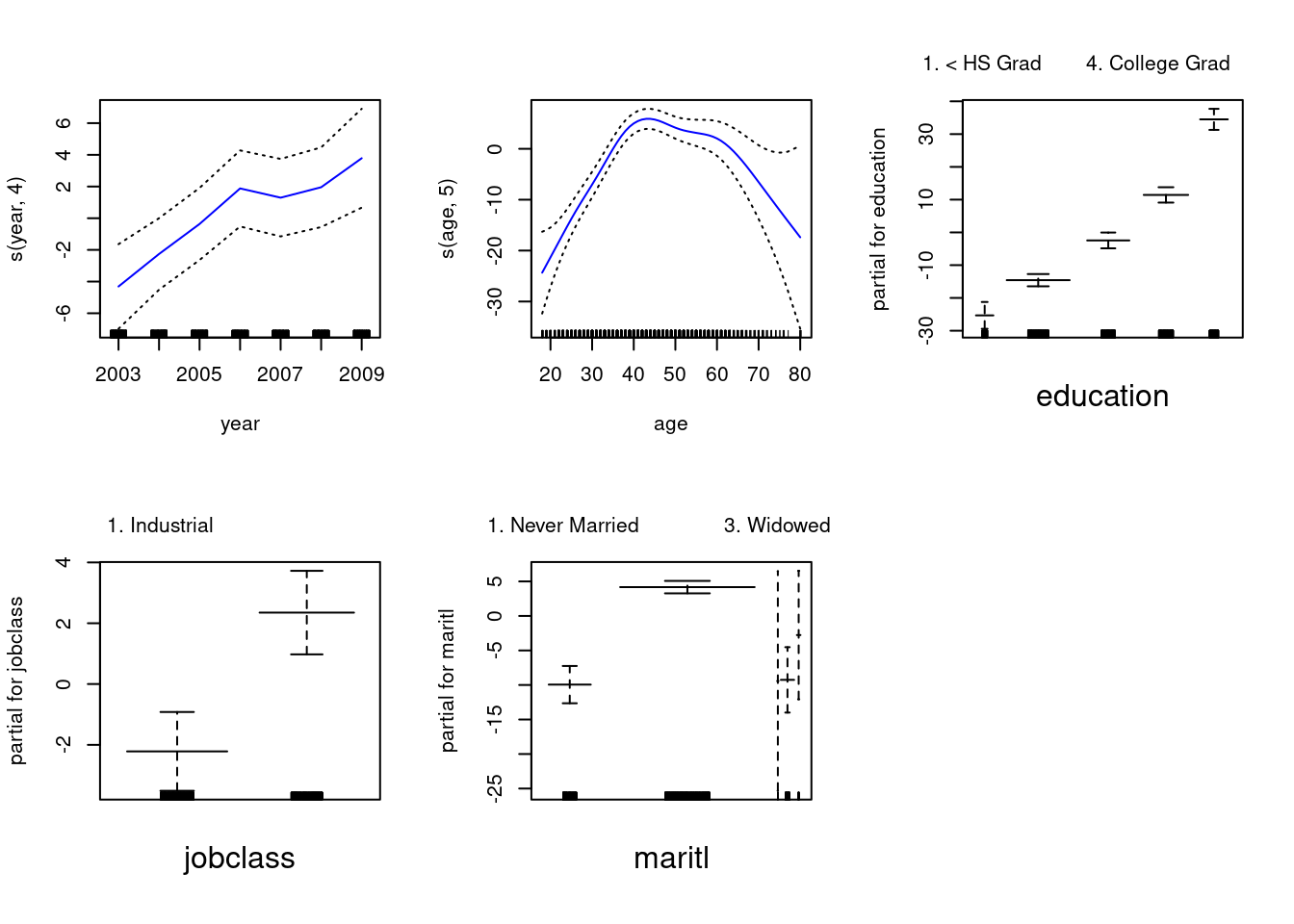
par(mfrow = c(2, 3))
plot(fit3, se = TRUE, col = "blue")

7.2.3 Question 8

Fit some of the non-linear models investigated in this chapter to the Auto data set. Is there evidence for non-linear relationships in this data set? Create some informative plots to justify your answer.

Here we want to explore a range of non-linear models. First let’s look at the relationships between the variables in the data.

pairs(Auto, cex = 0.4, pch = 19)

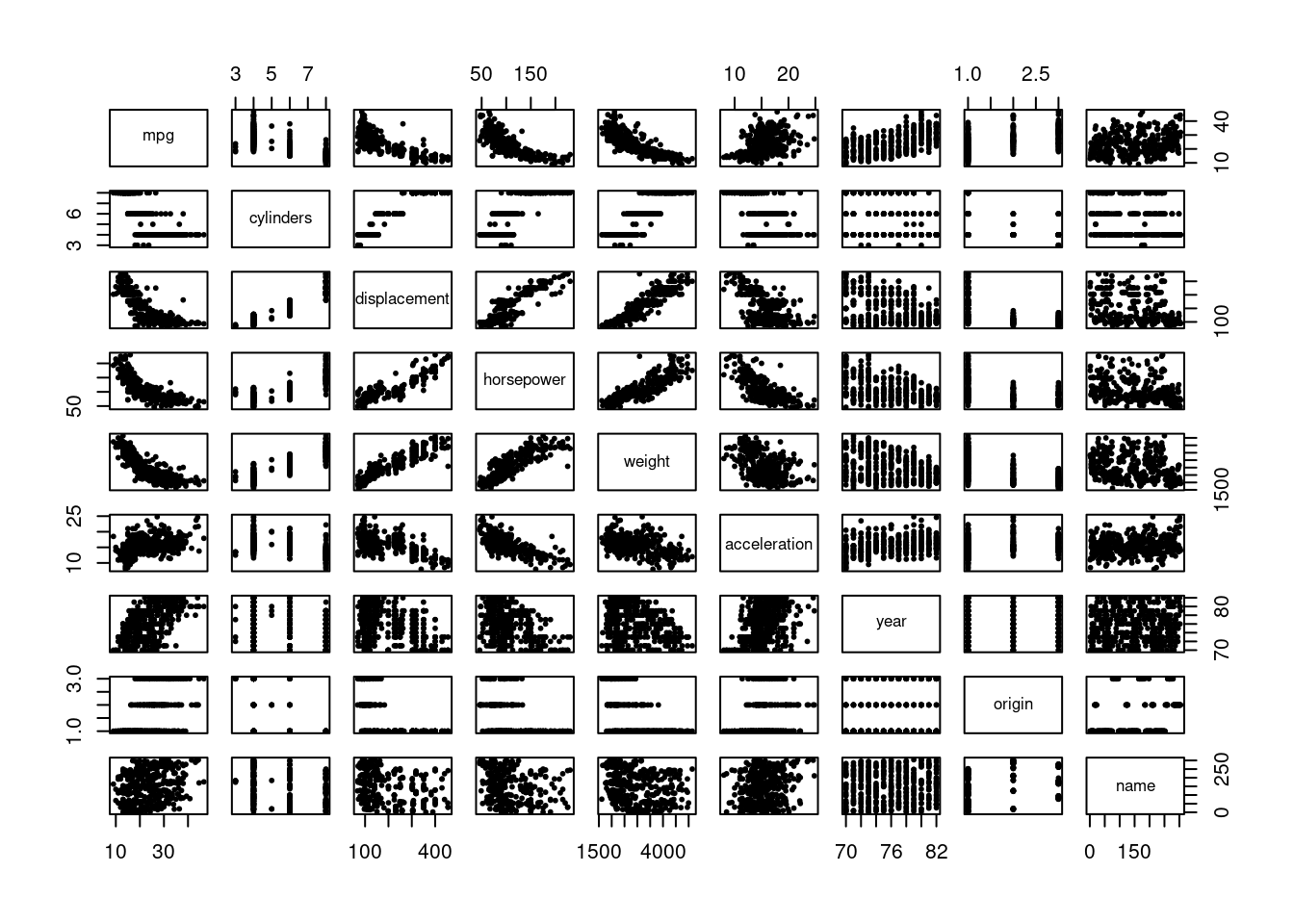
It does appear that there are some non-linear relationships (e.g. horsepower / weight and mpg). We will pick one variable (horsepower) to predict mpg and try the range of models discussed in this chapter. We will measure test MSE through cross-validation to compare the models.

library(tidyverse)
## ── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
## ✔ dplyr     1.1.4     ✔ readr     2.1.5
## ✔ forcats   1.0.0     ✔ stringr   1.5.1
## ✔ lubridate 1.9.3     ✔ tibble    3.2.1
## ✔ purrr     1.0.2     ✔ tidyr     1.3.1
## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## ✖ purrr::accumulate() masks foreach::accumulate()
## ✖ dplyr::filter()     masks stats::filter()
## ✖ dplyr::lag()        masks stats::lag()
## ✖ purrr::when()       masks foreach::when()
## ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors
set.seed(42)
fit <- glm(mpg ~ horsepower, data = Auto)
err <- cv.glm(Auto, fit, K = 10)$delta[1]

fit1 <- glm(mpg ~ poly(horsepower, 4), data = Auto)
err1 <- cv.glm(Auto, fit1, K = 10)$delta[1]

q <- quantile(Auto$horsepower)
Auto$hp_cats <- cut(Auto$horsepower, breaks = q, include.lowest = TRUE)
fit2 <- glm(mpg ~ hp_cats, data = Auto)
err2 <- cv.glm(Auto, fit2, K = 10)$delta[1]

fit3 <- glm(mpg ~ bs(horsepower, df = 4), data = Auto)
err3 <- cv.glm(Auto, fit3, K = 10)$delta[1]
## Warning in bs(horsepower, degree = 3L, knots = 92, Boundary.knots = c(46L, :
## some 'x' values beyond boundary knots may cause ill-conditioned bases
## Warning in bs(horsepower, degree = 3L, knots = 92, Boundary.knots = c(46L, :
## some 'x' values beyond boundary knots may cause ill-conditioned bases
fit4 <- glm(mpg ~ ns(horsepower, 4), data = Auto)
err4 <- cv.glm(Auto, fit4, K = 10)$delta[1]

fit5 <- gam(mpg ~ s(horsepower, df = 4), data = Auto)
# rough 10-fold cross-validation for gam.
err5 <- mean(replicate(10, {
  b <- cut(sample(seq_along(Auto$horsepower)), 10)
  pred <- numeric()
  for (i in 1:10) {
    train <- b %in% levels(b)[-i]
    f <- gam(mpg ~ s(horsepower, df = 4), data = Auto[train, ])
    pred[!train] <- predict(f, Auto[!train, ])
  }
  mean((Auto$mpg - pred)^2) # MSE
}))

c(err, err1, err2, err3, err4, err5)
## [1] 24.38418 19.94222 20.37940 18.92802 19.33556 19.02999
anova(fit, fit1, fit2, fit3, fit4, fit5)
## Analysis of Deviance Table
## 
## Model 1: mpg ~ horsepower
## Model 2: mpg ~ poly(horsepower, 4)
## Model 3: mpg ~ hp_cats
## Model 4: mpg ~ bs(horsepower, df = 4)
## Model 5: mpg ~ ns(horsepower, 4)
## Model 6: mpg ~ s(horsepower, df = 4)
##   Resid. Df Resid. Dev          Df Deviance      F    Pr(>F)    
## 1       390     9385.9                                          
## 2       387     7399.5  3.00000000  1986.39 35.258 < 2.2e-16 ***
## 3       388     7805.4 -1.00000000  -405.92 21.615 4.578e-06 ***
## 4       387     7276.5  1.00000000   528.94 28.166 1.880e-07 ***
## 5       387     7248.6  0.00000000    27.91                     
## 6       387     7267.7  0.00013612   -19.10                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
x <- seq(min(Auto$horsepower), max(Auto$horsepower), length.out=1000)
pred <- data.frame(
  x = x,
  "Linear" = predict(fit, data.frame(horsepower = x)),
  "Polynomial" = predict(fit1, data.frame(horsepower = x)),
  "Step" = predict(fit2, data.frame(hp_cats = cut(x, breaks = q, include.lowest = TRUE))),
  "Regression spline" = predict(fit3, data.frame(horsepower = x)),
  "Natural spline" = predict(fit4, data.frame(horsepower = x)),
  "Smoothing spline" = predict(fit5, data.frame(horsepower = x)),
  check.names = FALSE
)
pred <- pivot_longer(pred, -x)
ggplot(Auto, aes(horsepower, mpg)) +
  geom_point(color = alpha("steelblue", 0.4)) +
  geom_line(data = pred, aes(x, value, color = name)) +
  theme_bw()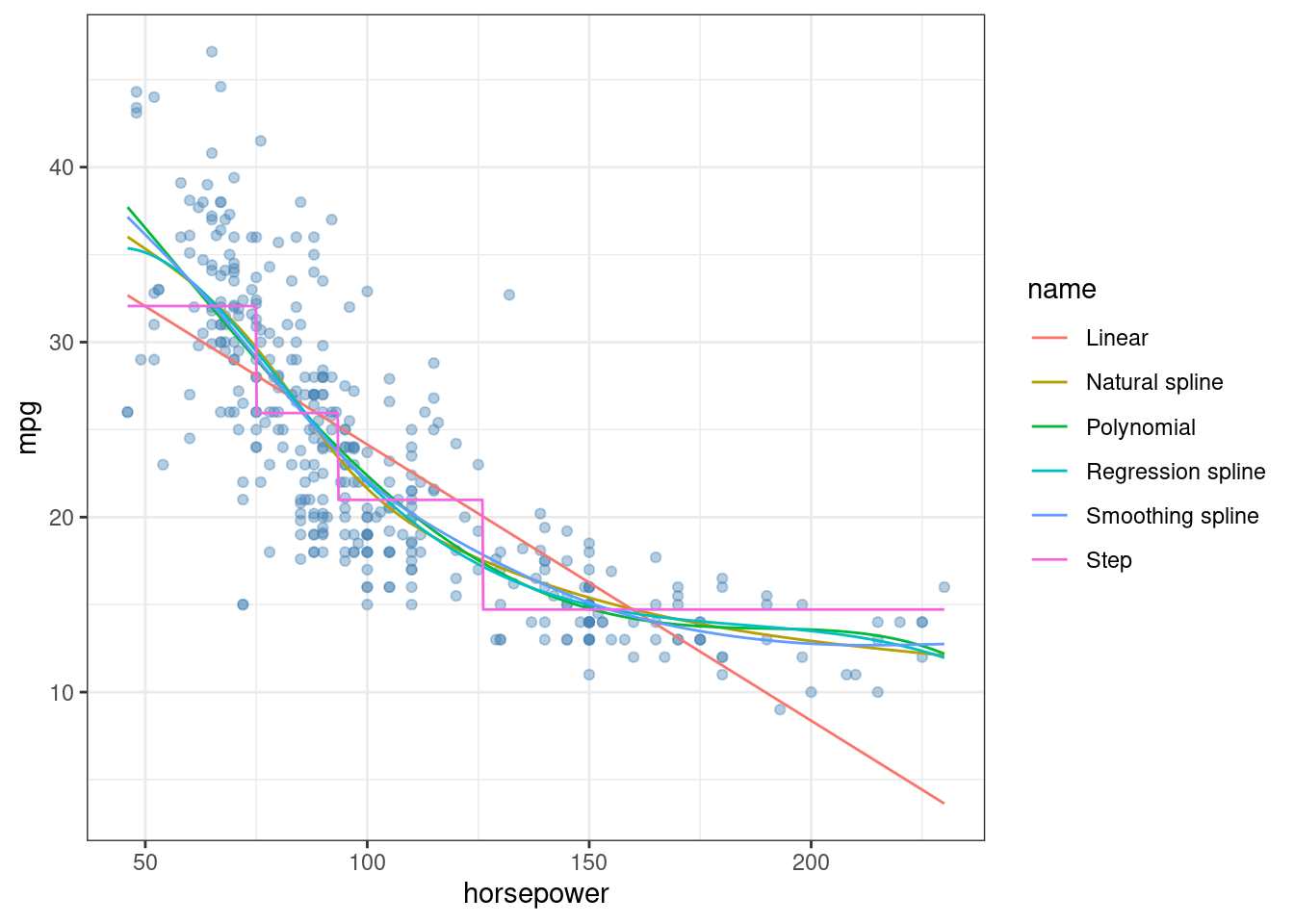

7.2.4 Question 9

This question uses the variables dis (the weighted mean of distances to five Boston employment centers) and nox (nitrogen oxides concentration in parts per 10 million) from the Boston data. We will treat dis as the predictor and nox as the response.

  1. Use the poly() function to fit a cubic polynomial regression to predict nox using dis. Report the regression output, and plot the resulting data and polynomial fits.
fit <- glm(nox ~ poly(dis, 3), data = Boston)
summary(fit)
## 
## Call:
## glm(formula = nox ~ poly(dis, 3), data = Boston)
## 
## Coefficients:
##                Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    0.554695   0.002759 201.021  < 2e-16 ***
## poly(dis, 3)1 -2.003096   0.062071 -32.271  < 2e-16 ***
## poly(dis, 3)2  0.856330   0.062071  13.796  < 2e-16 ***
## poly(dis, 3)3 -0.318049   0.062071  -5.124 4.27e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for gaussian family taken to be 0.003852802)
## 
##     Null deviance: 6.7810  on 505  degrees of freedom
## Residual deviance: 1.9341  on 502  degrees of freedom
## AIC: -1370.9
## 
## Number of Fisher Scoring iterations: 2
plot(nox ~ dis, data = Boston, col = alpha("steelblue", 0.4), pch = 19)
x <- seq(min(Boston$dis), max(Boston$dis), length.out = 1000)
lines(x, predict(fit, data.frame(dis = x)), col = "red", lty = 2)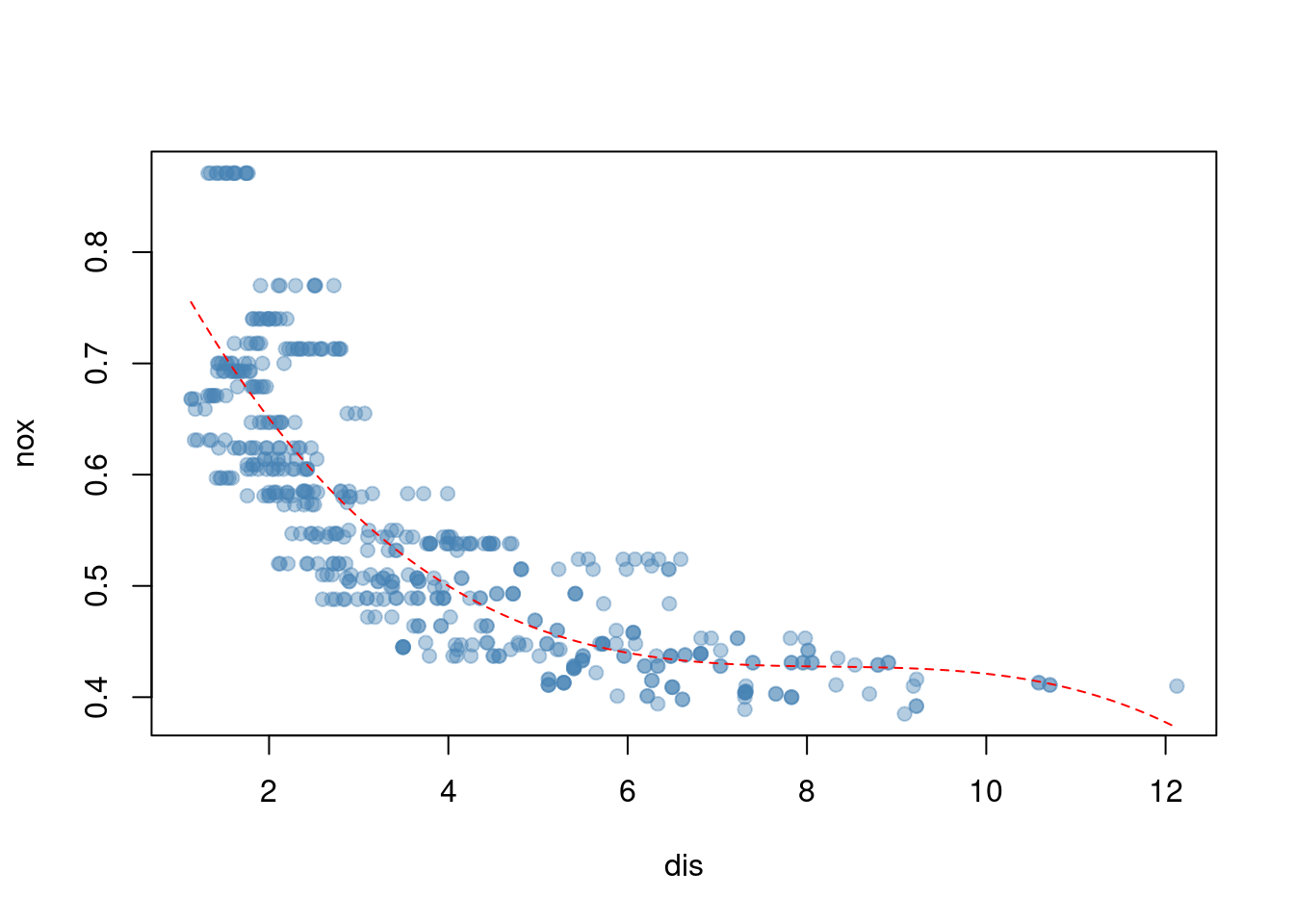

  1. Plot the polynomial fits for a range of different polynomial degrees (say, from 1 to 10), and report the associated residual sum of squares.
fits <- lapply(1:10, function(i) glm(nox ~ poly(dis, i), data = Boston))

x <- seq(min(Boston$dis), max(Boston$dis), length.out=1000)
pred <- data.frame(lapply(fits, function(fit) predict(fit, data.frame(dis = x))))
colnames(pred) <- 1:10
pred$x <- x
pred <- pivot_longer(pred, !x)
ggplot(Boston, aes(dis, nox)) +
  geom_point(color = alpha("steelblue", 0.4)) +
  geom_line(data = pred, aes(x, value, color = name)) +
  theme_bw()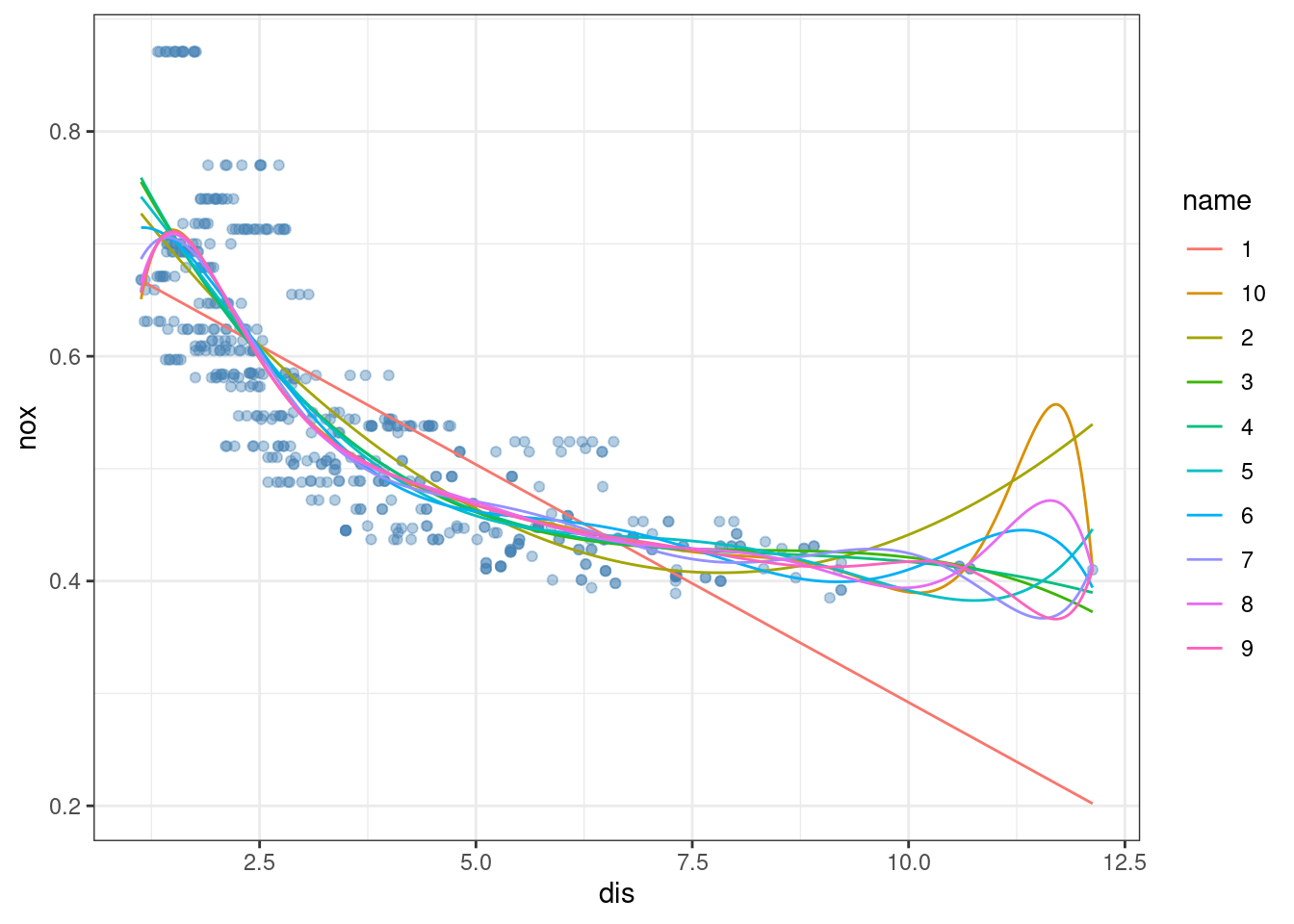

# residual sum of squares
do.call(anova, fits)[, 2]
##  [1] 2.768563 2.035262 1.934107 1.932981 1.915290 1.878257 1.849484 1.835630
##  [9] 1.833331 1.832171
  1. Perform cross-validation or another approach to select the optimal degree for the polynomial, and explain your results.
res <- sapply(1:10, function(i) {
  fit <- glm(nox ~ poly(dis, i), data = Boston)
  cv.glm(Boston, fit, K = 10)$delta[1]
})
which.min(res)
## [1] 4

The optimal degree is 3 based on cross-validation. Higher values tend to lead to overfitting.

  1. Use the bs() function to fit a regression spline to predict nox using dis. Report the output for the fit using four degrees of freedom. How did you choose the knots? Plot the resulting fit.
fit <- glm(nox ~ bs(dis, df = 4), data = Boston)
summary(fit)
## 
## Call:
## glm(formula = nox ~ bs(dis, df = 4), data = Boston)
## 
## Coefficients:
##                  Estimate Std. Error t value Pr(>|t|)    
## (Intercept)       0.73447    0.01460  50.306  < 2e-16 ***
## bs(dis, df = 4)1 -0.05810    0.02186  -2.658  0.00812 ** 
## bs(dis, df = 4)2 -0.46356    0.02366 -19.596  < 2e-16 ***
## bs(dis, df = 4)3 -0.19979    0.04311  -4.634 4.58e-06 ***
## bs(dis, df = 4)4 -0.38881    0.04551  -8.544  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for gaussian family taken to be 0.003837874)
## 
##     Null deviance: 6.7810  on 505  degrees of freedom
## Residual deviance: 1.9228  on 501  degrees of freedom
## AIC: -1371.9
## 
## Number of Fisher Scoring iterations: 2
plot(nox ~ dis, data = Boston, col = alpha("steelblue", 0.4), pch = 19)
x <- seq(min(Boston$dis), max(Boston$dis), length.out = 1000)
lines(x, predict(fit, data.frame(dis = x)), col = "red", lty = 2)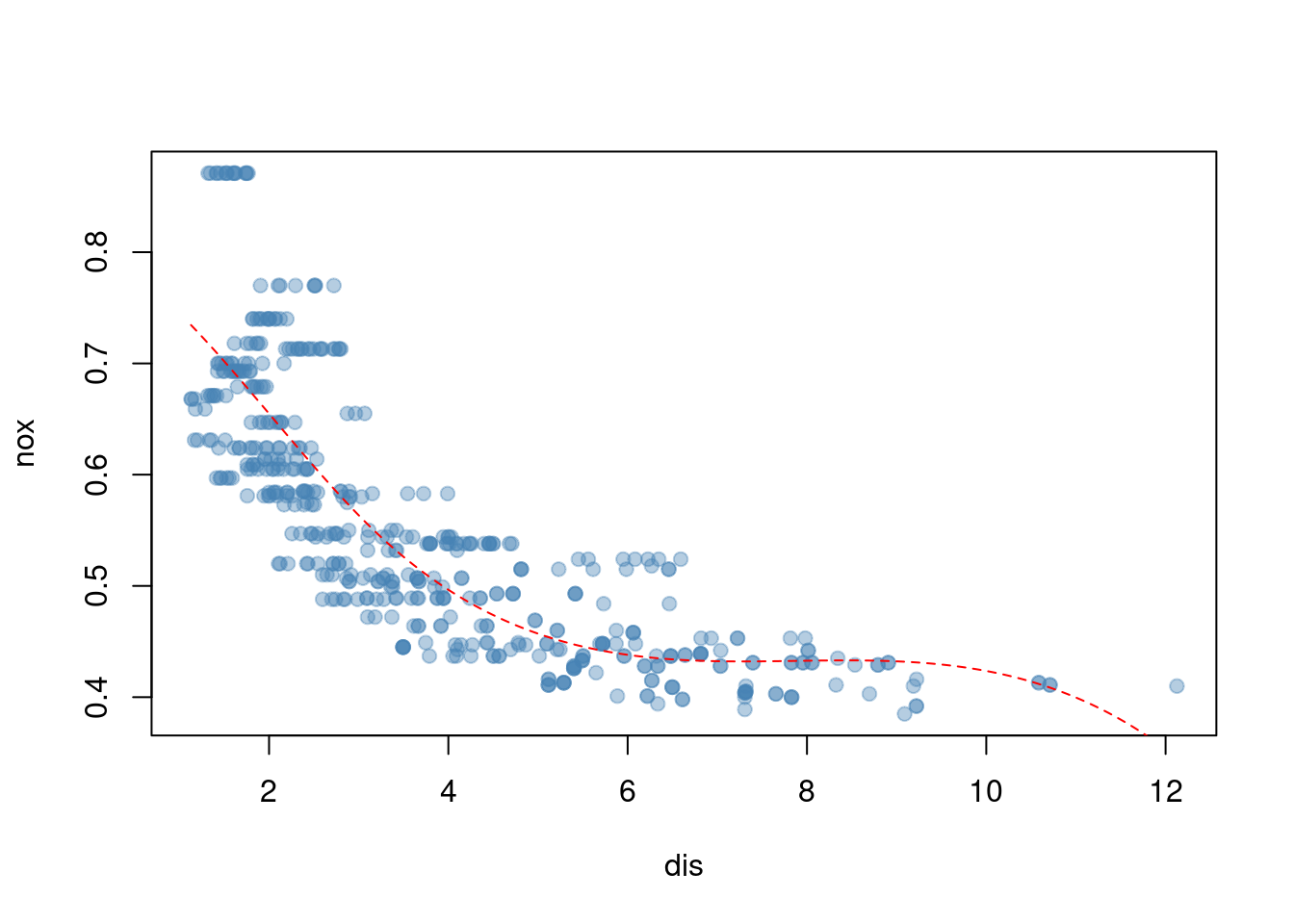

Knots are chosen based on quantiles of the data.

  1. Now fit a regression spline for a range of degrees of freedom, and plot the resulting fits and report the resulting RSS. Describe the results obtained.
fits <- lapply(3:10, function(i) {
  glm(nox ~ bs(dis, df = i), data = Boston)
})

x <- seq(min(Boston$dis), max(Boston$dis), length.out = 1000)
pred <- data.frame(lapply(fits, function(fit) predict(fit, data.frame(dis = x))))
colnames(pred) <- 3:10
pred$x <- x
pred <- pivot_longer(pred, !x)
ggplot(Boston, aes(dis, nox)) +
  geom_point(color = alpha("steelblue", 0.4)) +
  geom_line(data = pred, aes(x, value, color = name)) +
  theme_bw()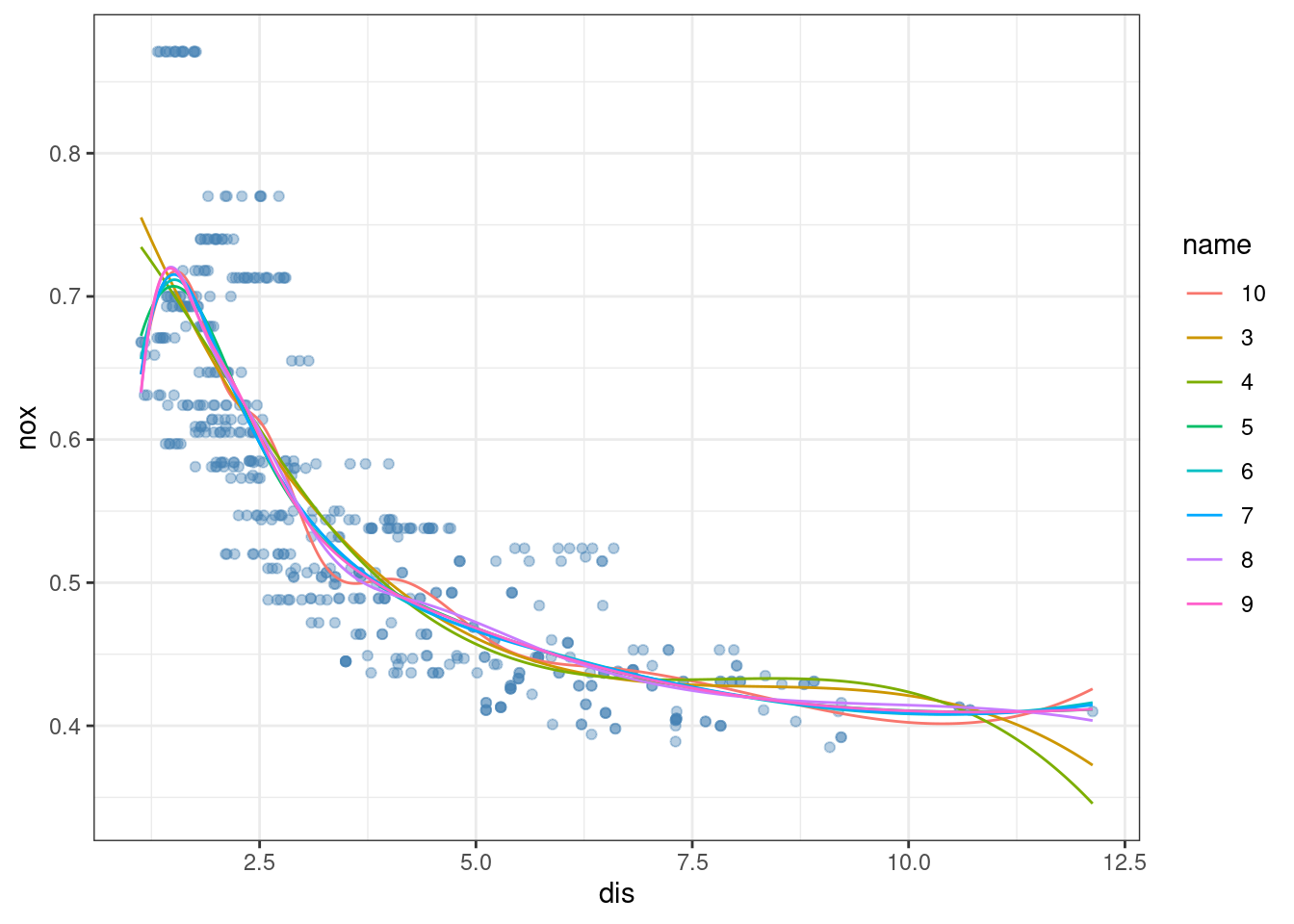

At high numbers of degrees of freedom the splines overfit the data (particularly at extreme ends of the distribution of the predictor variable).

  1. Perform cross-validation or another approach in order to select the best degrees of freedom for a regression spline on this data. Describe your results.
set.seed(42)
err <- sapply(3:10, function(i) {
  fit <- glm(nox ~ bs(dis, df = i), data = Boston)
  suppressWarnings(cv.glm(Boston, fit, K = 10)$delta[1])
})
which.min(err)
## [1] 8

This approach would select 4 degrees of freedom for the spline.

7.2.5 Question 10

This question relates to the College data set.

  1. Split the data into a training set and a test set. Using out-of-state tuition as the response and the other variables as the predictors, perform forward stepwise selection on the training set in order to identify a satisfactory model that uses just a subset of the predictors.
library(leaps)

# helper function to predict from a regsubsets model
predict.regsubsets <- function(object, newdata, id, ...) {
  form <- as.formula(object$call[[2]])
  mat <- model.matrix(form, newdata)
  coefi <- coef(object, id = id)
  xvars <- names(coefi)
  mat[, xvars] %*% coefi
}

set.seed(42)
train <- rep(TRUE, nrow(College))
train[sample(1:nrow(College), nrow(College) * 1 / 3)] <- FALSE
fit <- regsubsets(Outstate ~ ., data = College[train, ], nvmax = 17, method = "forward")

plot(summary(fit)$bic, type = "b")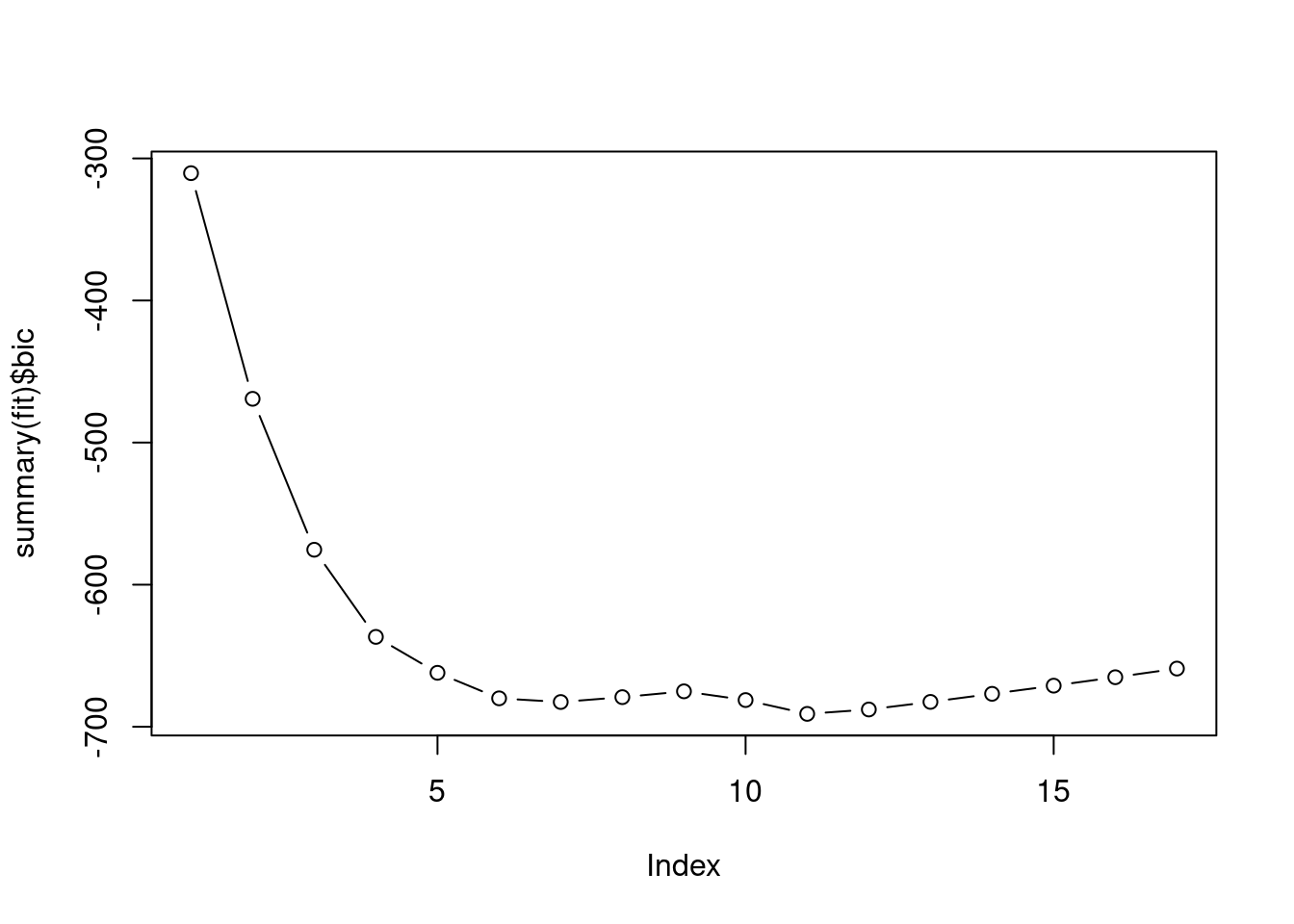

which.min(summary(fit)$bic)
## [1] 11
# or via cross-validation
err <- sapply(1:17, function(i) {
  x <- coef(fit, id = i)
  mean((College$Outstate[!train] - predict(fit, College[!train, ], i))^2)
})
which.min(err)
## [1] 16
min(summary(fit)$bic)
## [1] -690.9375

For the sake of simplicity we’ll choose 6

coef(fit, id = 6)
##   (Intercept)    PrivateYes    Room.Board           PhD   perc.alumni 
## -3540.0544008  2736.4231642     0.9061752    33.7848157    47.1998115 
##        Expend     Grad.Rate 
##     0.2421685    33.3137332
  1. Fit a GAM on the training data, using out-of-state tuition as the response and the features selected in the previous step as the predictors. Plot the results, and explain your findings.
fit <- gam(Outstate ~ Private + s(Room.Board, 2) + s(PhD, 2) + s(perc.alumni, 2) +
  s(Expend, 2) + s(Grad.Rate, 2), data = College[train, ])
  1. Evaluate the model obtained on the test set, and explain the results obtained.
pred <- predict(fit, College[!train, ])
err_gam <- mean((College$Outstate[!train] - pred)^2)
plot(err, ylim = c(min(err_gam, err), max(err)), type = "b")
abline(h = err_gam, col = "red", lty = 2)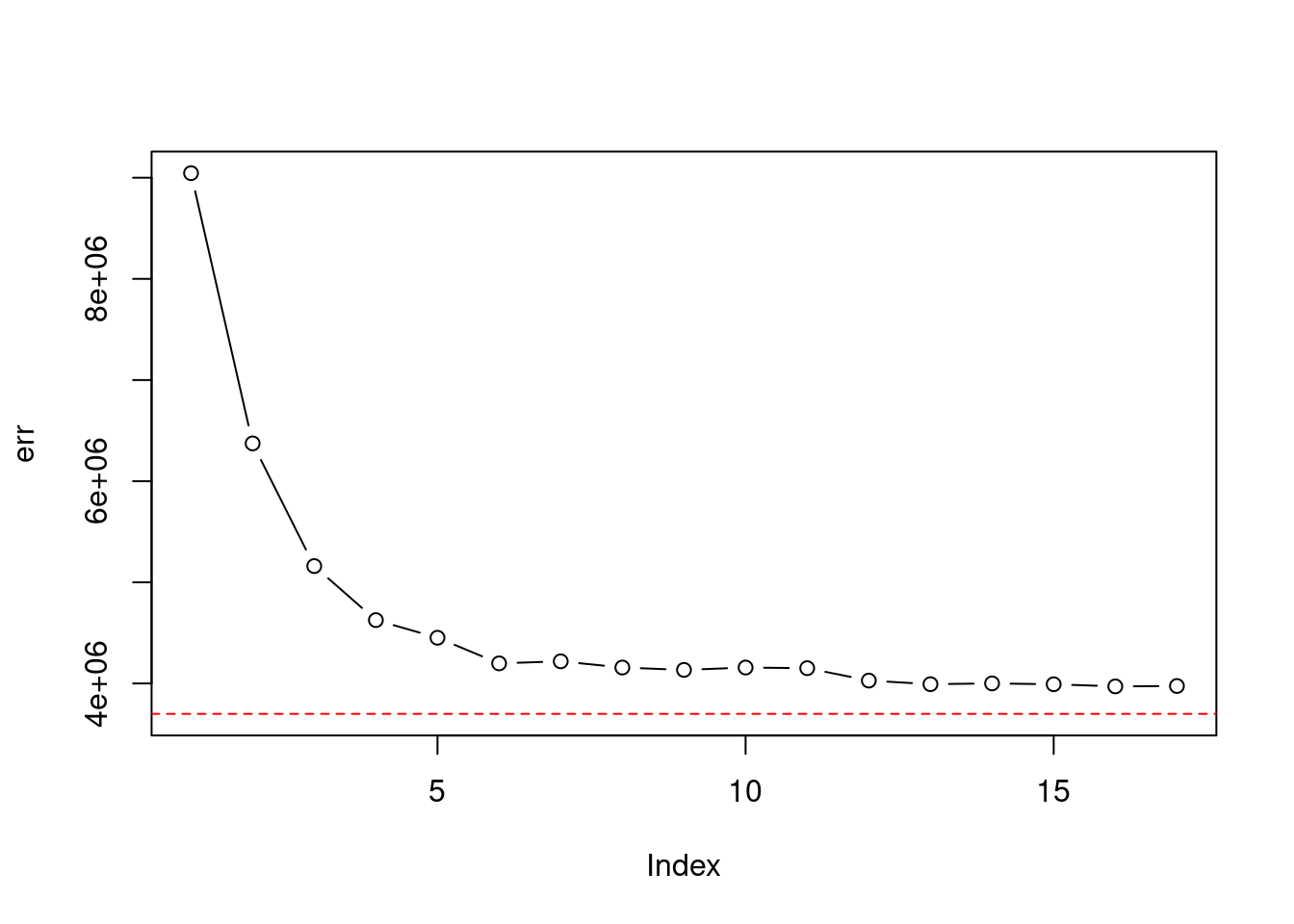

# r-squared
1 - err_gam / mean((College$Outstate[!train] - mean(College$Outstate[!train]))^2)
## [1] 0.7655905
  1. For which variables, if any, is there evidence of a non-linear relationship with the response?
summary(fit)
## 
## Call: gam(formula = Outstate ~ Private + s(Room.Board, 2) + s(PhD, 
##     2) + s(perc.alumni, 2) + s(Expend, 2) + s(Grad.Rate, 2), 
##     data = College[train, ])
## Deviance Residuals:
##      Min       1Q   Median       3Q      Max 
## -7112.59 -1188.98    33.13  1238.54  8738.65 
## 
## (Dispersion Parameter for gaussian family taken to be 3577008)
## 
##     Null Deviance: 8471793308 on 517 degrees of freedom
## Residual Deviance: 1809966249 on 506.0001 degrees of freedom
## AIC: 9300.518 
## 
## Number of Local Scoring Iterations: NA 
## 
## Anova for Parametric Effects
##                    Df     Sum Sq    Mean Sq F value    Pr(>F)    
## Private             1 2327235738 2327235738 650.610 < 2.2e-16 ***
## s(Room.Board, 2)    1 1741918028 1741918028 486.976 < 2.2e-16 ***
## s(PhD, 2)           1  668408518  668408518 186.863 < 2.2e-16 ***
## s(perc.alumni, 2)   1  387819183  387819183 108.420 < 2.2e-16 ***
## s(Expend, 2)        1  625813340  625813340 174.954 < 2.2e-16 ***
## s(Grad.Rate, 2)     1  111881207  111881207  31.278 3.664e-08 ***
## Residuals         506 1809966249    3577008                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Anova for Nonparametric Effects
##                   Npar Df Npar F     Pr(F)    
## (Intercept)                                   
## Private                                       
## s(Room.Board, 2)        1  2.224   0.13648    
## s(PhD, 2)               1  5.773   0.01664 *  
## s(perc.alumni, 2)       1  0.365   0.54581    
## s(Expend, 2)            1 61.182 3.042e-14 ***
## s(Grad.Rate, 2)         1  4.126   0.04274 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Non-linear relationships are significant for Expend and PhD.

7.2.6 Question 11

In Section 7.7, it was mentioned that GAMs are generally fit using a backfitting approach. The idea behind backfitting is actually quite simple. We will now explore backfitting in the context of multiple linear regression.

Suppose that we would like to perform multiple linear regression, but we do not have software to do so. Instead, we only have software to perform simple linear regression. Therefore, we take the following iterative approach: we repeatedly hold all but one coefficient estimate fixed at its current value, and update only that coefficient estimate using a simple linear regression. The process is continued until convergence—that is, until the coefficient estimates stop changing.

We now try this out on a toy example.

  1. Generate a response \(Y\) and two predictors \(X_1\) and \(X_2\), with \(n = 100\).
set.seed(42)
x1 <- rnorm(100)
x2 <- rnorm(100)
y <- 2 + 0.2 * x1 + 4 * x2 + rnorm(100)
  1. Initialize \(\hat{\beta}_1\) to take on a value of your choice. It does not matter 1 what value you choose.
beta1 <- 20

  1. Keeping \(\hat{\beta}_1\) fixed, fit the model \[Y - \hat{\beta}_1X_1 = \beta_0 + \beta_2X_2 + \epsilon.\] You can do this as follows:

    > a <- y - beta1 * x1
> beta2 <- lm(a ~ x2)$coef[2]
a <- y - beta1*x1
beta2 <- lm(a ~ x2)$coef[2]

  1. Keeping \(\hat{\beta}_2\) fixed, fit the model \[Y - \hat{\beta}_2X_2 = \beta_0 + \beta_1 X_1 + \epsilon.\] You can do this as follows:

    > a <- y - beta2 * x2
> beta1 <- lm(a ~ x1)$coef[2]
a <- y - beta2 * x2
beta1 <- lm(a ~ x1)$coef[2]
  1. Write a for loop to repeat (c) and (d) 1,000 times. Report the estimates of \(\hat{\beta}_0, \hat{\beta}_1,\) and \(\hat{\beta}_2\) at each iteration of the for loop. Create a plot in which each of these values is displayed, with \(\hat{\beta}_0, \hat{\beta}_1,\) and \(\hat{\beta}_2\) each shown in a different color.
res <- matrix(NA, nrow = 1000, ncol = 3)
colnames(res) <- c("beta0", "beta1", "beta2")
beta1 <- 20
for (i in 1:1000) {
  beta2 <- lm(y - beta1*x1 ~ x2)$coef[2]
  beta1 <- lm(y - beta2*x2 ~ x1)$coef[2]
  beta0 <- lm(y - beta2*x2 ~ x1)$coef[1]
  res[i, ] <- c(beta0, beta1, beta2)
}
res <- as.data.frame(res)
res$Iteration <- 1:1000
res <- pivot_longer(res, !Iteration)
p <- ggplot(res, aes(x=Iteration, y=value, color=name)) +
  geom_line() +
  geom_point() +
  scale_x_continuous(trans = "log10")
p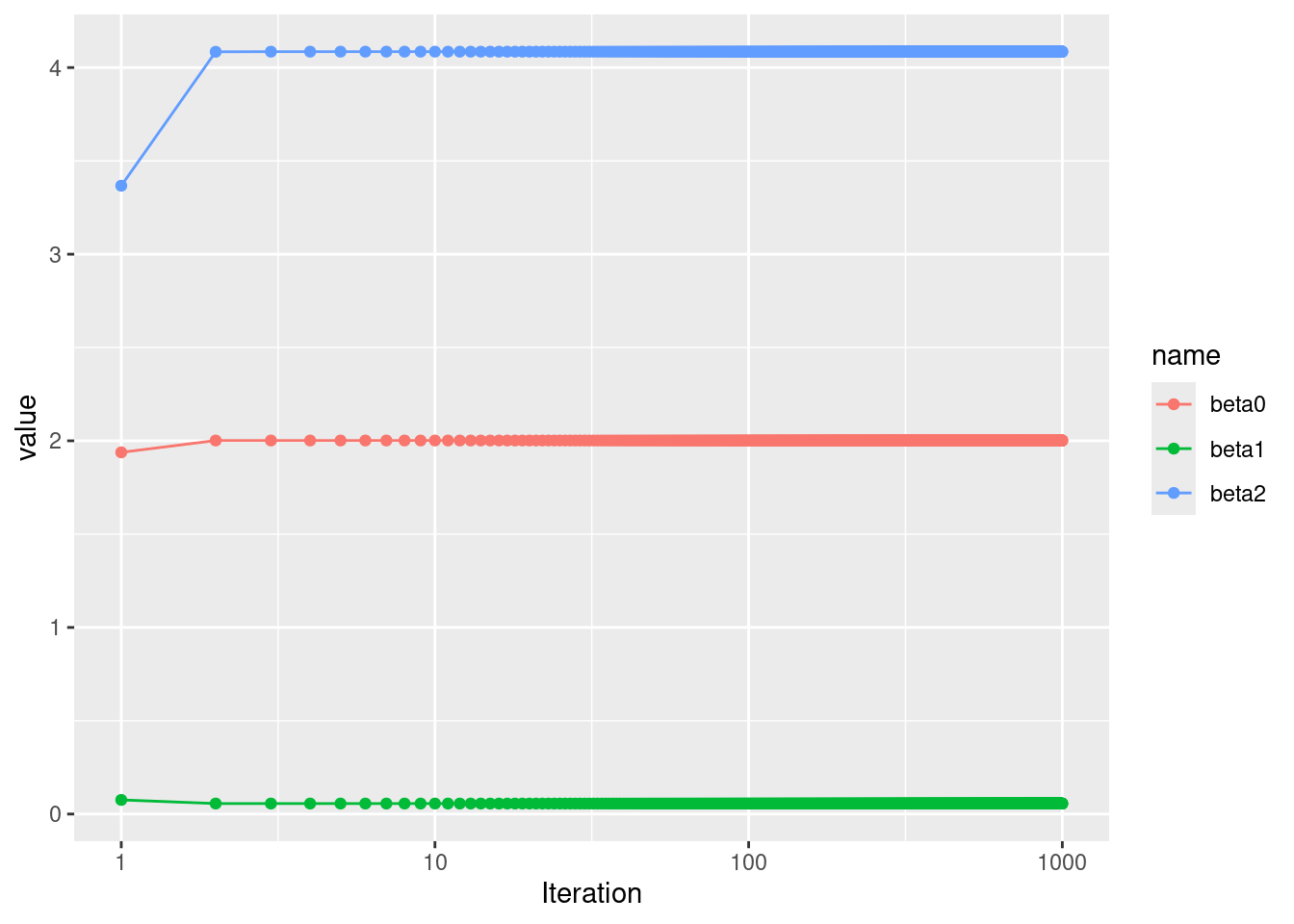

  1. Compare your answer in (e) to the results of simply performing multiple linear regression to predict \(Y\) using \(X_1\) and \(X_2\). Use the abline() function to overlay those multiple linear regression coefficient estimates on the plot obtained in (e).
fit <- lm(y ~ x1 + x2)
coef(fit)
## (Intercept)          x1          x2 
##  2.00176627  0.05629075  4.08529318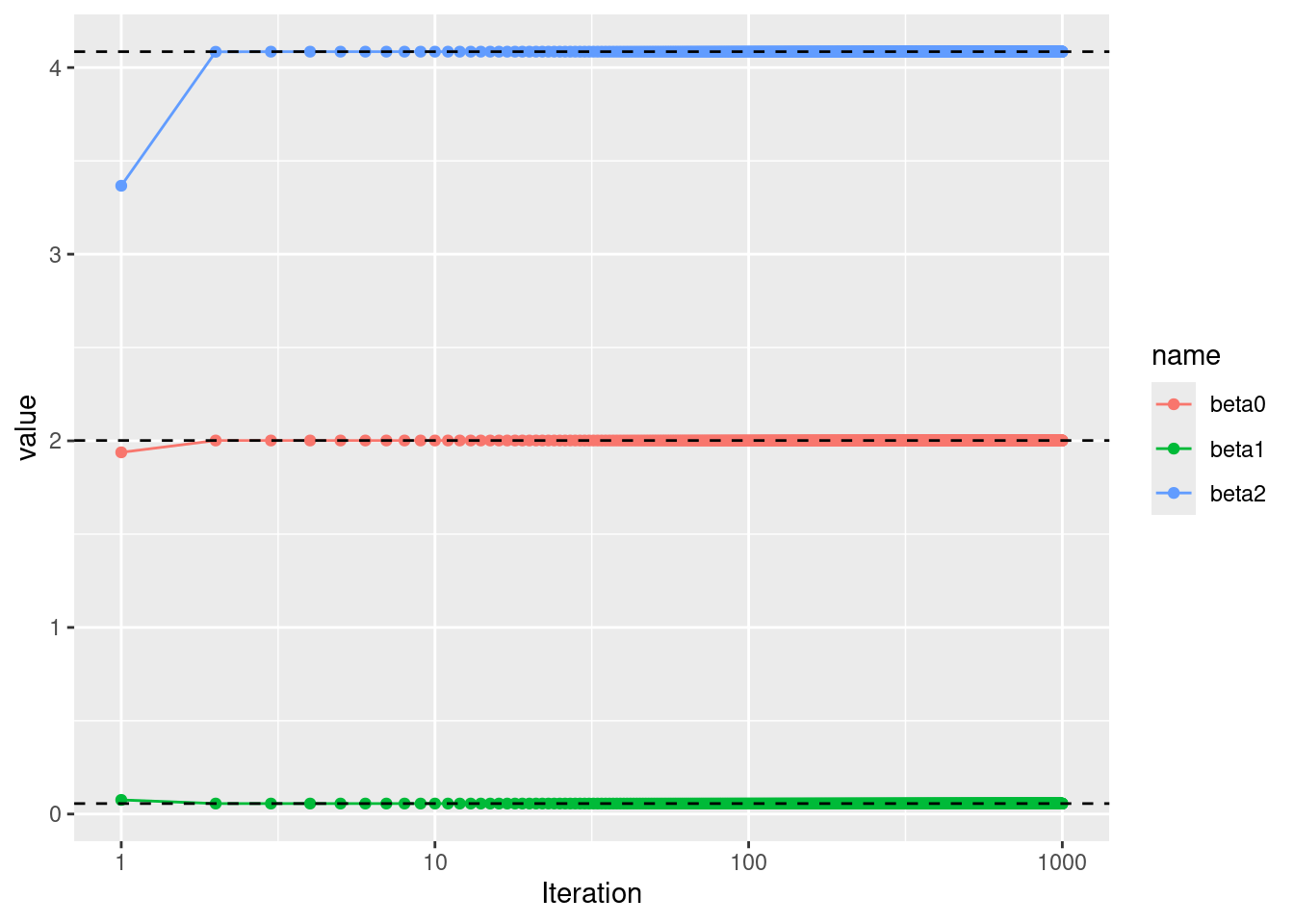
p + geom_hline(yintercept = coef(fit), lty = 2)

  1. On this data set, how many backfitting iterations were required in order to obtain a “good” approximation to the multiple regression coefficient estimates?

In this case, good estimates were obtained after 3 iterations.

7.2.7 Question 12

This problem is a continuation of the previous exercise. In a toy example with \(p = 100\), show that one can approximate the multiple linear regression coefficient estimates by repeatedly performing simple linear regression in a backfitting procedure. How many backfitting iterations are required in order to obtain a “good” approximation to the multiple regression coefficient estimates? Create a plot to justify your answer.

set.seed(42)

p <- 100
n <- 1000

betas <- rnorm(p) * 5
x <- matrix(rnorm(n * p), ncol = p, nrow = n)
y <- (x %*% betas) + rnorm(n)  # ignore beta0 for simplicity

# multiple regression
fit <- lm(y ~ x - 1)
coef(fit)
##          x1          x2          x3          x4          x5          x6 
##   6.9266184  -2.8428817   1.8686821   3.1466472   1.9601927  -0.5529214 
##          x7          x8          x9         x10         x11         x12 
##   7.4786723  -0.4454637  10.0816005  -0.2391234   6.5832468  11.4451280 
##         x13         x14         x15         x16         x17         x18 
##  -6.9684368  -1.3604495  -0.6310041   3.1786639  -1.4470502 -13.2957027 
##         x19         x20         x21         x22         x23         x24 
## -12.2061834   6.5765842  -1.5227262  -8.8855906  -0.8422954   6.1189230 
##         x25         x26         x27         x28         x29         x30 
##   9.4395267  -2.1697854  -1.2738835  -8.8457987   2.2851699  -3.1922704 
##         x31         x32         x33         x34         x35         x36 
##   2.2812995   3.4695892   5.1162617  -3.0423873   2.4985589  -8.5952764 
##         x37         x38         x39         x40         x41         x42 
##  -3.9539370  -4.2616463 -12.0038342   0.1981058   1.0559250  -1.8205017 
##         x43         x44         x45         x46         x47         x48 
##   3.7739990  -3.6240020  -6.8575534   2.1042998  -4.0228773   7.1880298 
##         x49         x50         x51         x52         x53         x54 
##  -2.1967821   3.3137115   1.6406524  -3.9402065   7.9067705   3.1815846 
##         x55         x56         x57         x58         x59         x60 
##   0.4504175   1.4003479   3.3999814   0.4317695 -14.9255798   1.3816878 
##         x61         x62         x63         x64         x65         x66 
##  -1.8071634   0.9907740   2.9771540   6.9528872  -3.5956916   6.5283946 
##         x67         x68         x69         x70         x71         x72 
##   1.6798820   5.1911857   4.5573256   3.5961319  -5.1909352  -0.4869003 
##         x73         x74         x75         x76         x77         x78 
##   3.1472166  -4.7898363  -2.7402076   2.9247173   3.8659938   2.3686379 
##         x79         x80         x81         x82         x83         x84 
##  -4.4261734  -5.5020688   7.5807239   1.3010702   0.4378713  -0.5856580 
##         x85         x86         x87         x88         x89         x90 
##  -5.9799328   3.0089329  -1.1230969  -0.8857679   4.7211363   4.1042952 
##         x91         x92         x93         x94         x95         x96 
##   6.9492037  -2.3959211   3.2188522   6.9947040  -5.5392641  -4.3114784 
##         x97         x98         x99        x100 
##  -5.7287292  -7.3148812   0.3454408   3.2830658
# backfitting
backfit <- function(x, y, iter = 20) {
  beta <- matrix(0, ncol = ncol(x), nrow = iter + 1)
  for (i in 1:iter) {
    for (k in 1:ncol(x)) {
      residual <- y - (x[, -k] %*% beta[i, -k])
      beta[i + 1, k] <- lm(residual ~ x[, k])$coef[2]
    }
  }
  beta[-1, ]
}
res <- backfit(x, y)
error <- rowMeans(sweep(res, 2, betas)^2)
plot(error, log = "x", type = "b")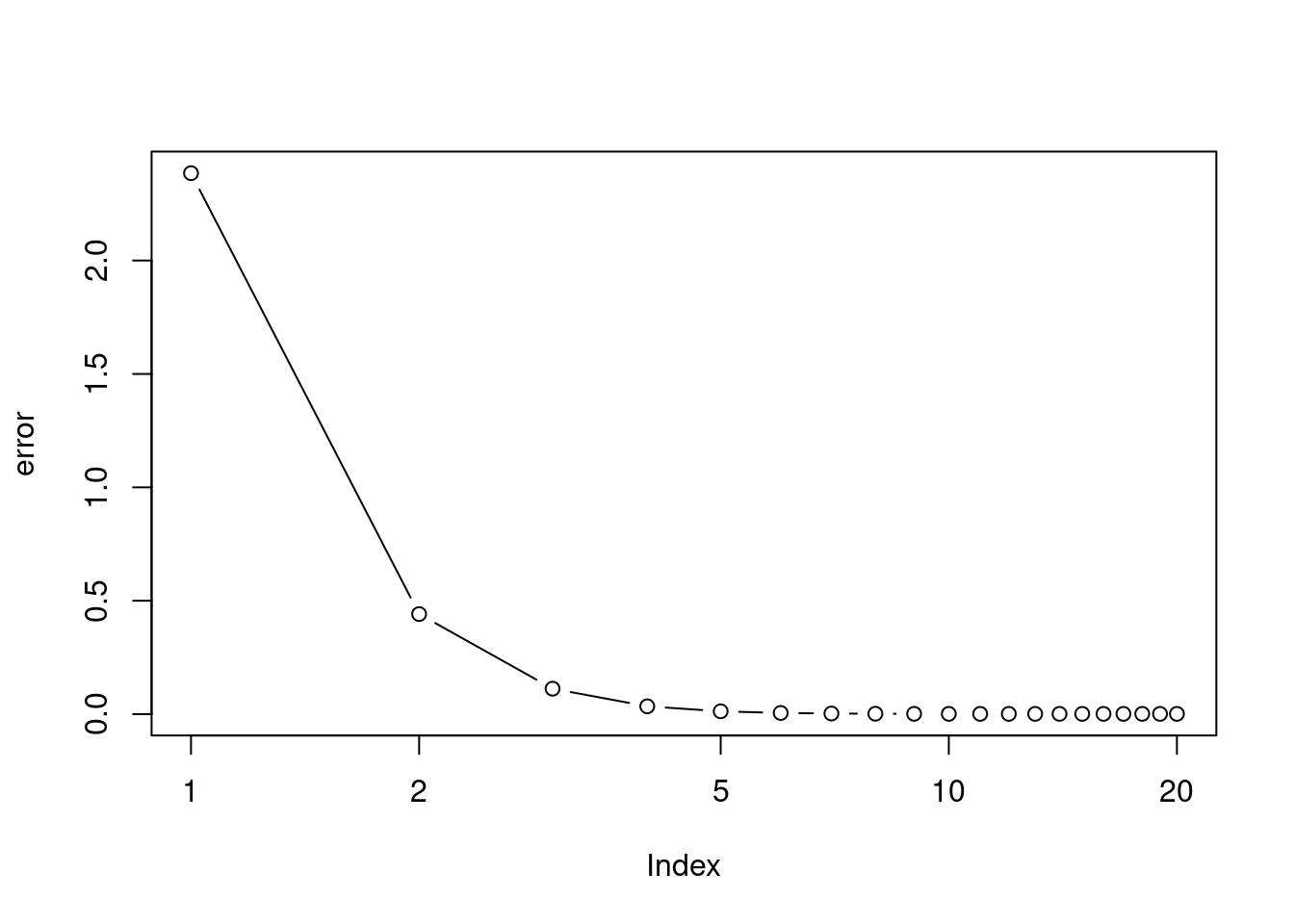

# backfitting error
error[length(error)]
## [1] 0.001142494
# lm error
mean((coef(fit) - betas)^2)
## [1] 0.001138655

We need around 5 to 6 iterations to obtain a good estimate of the coefficients.